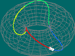
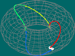
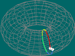
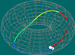
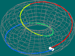
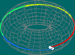
Numa superfície, fixando os pontos inicial e final, podemos considerar o conjunto das classes de homotopia dos caminhos entre esses dois pontos. Se os pontos coincidirem (isto é, se os caminhos forem fechados), podemos operar elementos desse conjunto, pois o ponto final de um caminho é o ponto inicial de outro. E, além disso, o caminho produto que daí resulta é, ainda, um caminho fechado a partir do ponto considerado – matematicamente, diz-se que a operação é fechada para o conjunto. Sabemos também que a operação é associativa, tem elemento neutro e todo o elemento tem inverso no conjunto (pois o ponto inicial e final são iguais). Assim, o conjunto das classes de homotopia de caminhos fechados a partir de um ponto – ponto básico – (com a operação) diz-se, matematicamente, um grupo, designado por grupo fundamental do espaço relativamente ao ponto.
Mostra-se que, nas superfícies conexas por caminhos (como são todas as que considerámos), o grupo fundamental não varia com a escolha do ponto básico (a menos de um isomorfismo) e, portanto, faz sentido falar em grupo fundamental da superfície. E, depois de analisar o grupo fundamental da superfície, é útil, se possível, identificar uma estrutura de grupo já conhecida que lhe seja isomorfa.
|
Plano |
 0 |
|||||||
|
Esfera |
 0 |
|||||||
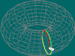
| Cilindro |
... |
 -2 |
 -1 |
 0 |
 1 |
 2 |
 3 |
... |
,+}|
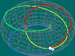
Toro |
... |
... |
... |
... |
... |
... |
... |
... |
|
... |
|
 (-1,2) |
 (0,2) |
 (1,2) |
 (2,2) |
 (3,2) |
... |
|
|
... |
 (-2,1) |
 (-1,1) |
 (0,1) |
 (1,1) |
 (2,1) |
 (3,1) |
... |
|
|
... |
 (-2,0) |
 (-1,0) |
 (0,0) |
 (1,0) |
 (2,0) |
 (3,0) |
... |
|
|
... |
 (-2,-1) |
 (-1,-1) |
 (0,-1) |
 (1,-1) |
 (2,-1) |
 (3,-1) |
... |
|
|
... |
... |
... |
... |
... |
... |
... |
... |
