| PLANO
PROJECTIVO –
grupo fundamental |
| PLANO
PROJECTIVO –
grupo fundamental |
No plano projectivo, o tratamento das homotopias não é intuitivamente tão simples como no plano e na esfera. Mas um dos modelos do plano projectivo é uma esfera com os pontos diametralmente opostos identificados. Cada caminho na esfera projecta-se naturalmente num caminho no espaço projectivo, podendo dizer-se que aquele é um levantamento deste. Dado um caminho no plano projectivo, ele admite dois levantamentos na esfera mas, uma vez fixado um dos dois pontos que se projectam na sua origem como ponto inicial na esfera, o levantamento do caminho é único.
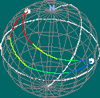 |
Se
considerarmos dois caminhos no espaço projectivo entre os mesmos
pontos, temos, neste modelo, duas opções: escolhendo dois
levantamentos na esfera com o mesmo ponto inicial, ou os pontos finais
na esfera são os mesmos ou são diametralmente opostos.
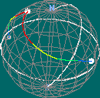
Se forem os mesmos, estamos no caso da esfera simples: quaisquer dois
caminhos com os mesmos pontos inicial e final sobre a esfera são
homotópicos e uma homotopia na esfera projecta-se naturalmente
numa homotopia no espaço projectivo. Se forem diametralmente
opostos, pode provar-se que não existe uma deformação
contínua entre eles no espaço projectivo. Esta ideia pode
ser explorada de forma intuitiva no applet. |
 |
Analisando o grupo fundamental,
ou seja, considerando apenas os caminhos fechados sobre o plano projectivo,
o ponto final do caminho, na esfera, ou é igual ao ponto inicial –
caminho fechado –, ou é o seu antípoda – caminho
aberto. No primeiro caso, temos um caminho fechado sobre a esfera, que pode
ser contraído num ponto (caminho constante) – representante “mais
simples” da classe. No segundo caso, o caminho sobre a esfera não
é fechado, não sendo, portanto, homotópico a um ponto.
Neste caso, o representante “mais simples” da classe é
o arco de círculo máximo que une o ponto inicial ao seu antípoda.
Assim, o grupo fundamental do plano projectivo tem apenas dois elementos.
Desta forma, dizemos que há uma correspondência entre o conjunto
das suas classes de homotopia e o conjunto {0,1}
– o grupo fundamental do plano projectivo
é isomorfo a ![]() 2.
2.