| OPERAÇÃO |
Se
durante uma hora percorrermos um caminho e durante outra hora percorrermos
outro, o que acontece se apenas numa hora quisermos percorrer os dois?
A resposta é simples: temos de seguir os mesmos trilhos, mas
mais depressa! O primeiro caminho, que havia sido percorrido numa hora,
agora tem de ser percorrido em meia, para que ainda nos reste outro
tanto de tempo para o segundo caminho. |
Este é o princípio da operação de caminhos. Dados dois caminhos contíguos (ou seja, em que o início do segundo coincide com o fim do primeiro), o caminho produto corresponde ao percurso consecutivo de cada um deles com o dobro da velocidade. Note-se que a contiguidade dos caminhos é importante para garantir a continuidade do caminho produto e o aumento da velocidade impõe-se pois queremos que o tempo total (o domínio) se mantenha.
Matematicamente, dizemos que, dados dois caminhos f1 e f2 de [0,1] em S, com f2(0)=f1(1), g=f1.f2 é um caminho de [0,1] em S tal que:
| g(t) = | f1(2t) | se | 0
|
= | f1(2t) | se | 0
|
|||||
| f2(2(t–0.5)) | se | 0.5
< t |
f2(2t–1) | se | 0.5
< t |
|||||||
|
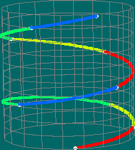
Se pensarmos nos elásticos graduados, a questão põe-se em como fazer com que apenas com um elástico possamos percorrer os pontos antes percorridos com dois elásticos (do mesmo comprimento). E a resposta é, mais uma vez, simples: temos de esticar o elástico! Nos applets que se seguem, o esticar do elástico é visível na coloração; admitindo que inicialmente os elásticos são todos iguais, se uma cor fica visível num maior comprimento isso significa que o elástico está mais esticado nessa zona. |
|
|
(Clique sobre a figura para aceder
ao applet.) |
Uma
chamada de atenção para as proporções do
aumento da velocidade. No que dissemos, a velocidade dobra para cada
um dos caminhos, mas, à partida, não teria de ser obrigatoriamente
assim... Ao dispormos de uma hora, podíamos, por exemplo, percorrer
o primeiro caminho em três quartos de hora e o segundo apenas
em 15 min... Aqui a relação das velocidades seria diferente;
já não seria de 2:1 em ambos os caminhos, mas sim de 4:3
no primeiro e e de 4:1 no segundo, e o caminho final seria diferente
daquele obtido pela transformação acima! No entanto, os
dois resultados são homotópicos (por uma homotopia apenas
de coloração). A escolha pela proporção
2:1 acima é preferida por ser a mais natural. |
Analisemos agora três propriedades básicas da operação nas classes de homotopia.
| [Descrição da operação] |