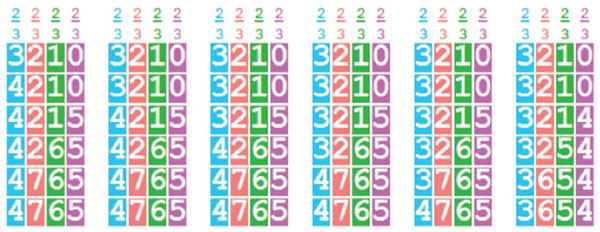
Para uma versão virtual deste módulo, interessa dispor de vários ciclos não-transitivos diferentes, todos ótimos (no sentido de a probabilidade mínima ser a maior possível⁴). Isso não é viável para dados com 0 a 6 pintas nas faces, pois já vimos que só há um ciclo ótimo, o acima indicado. Mas recorrendo a dados com faces podendo ter maior número de pintas e mantendo as outras características (em particular, ser 2 o número máximo de faces diferentes em cada dado), é possível obter mais ciclos ótimos. Com o Mathematica foi possível localizar 13 ciclos ótimos para 0 a 7 pintas e 81 para 0 a 8 pintas (num total, respetivamente, de 527 e 3495 ciclos não-transitivos). Na figura 6, eis os ciclos ótimos com 0 a 7 pintas.

Fig 6

Se, em vez de ciclos de quatro dados, nos limitarmos a ciclos de três, digamos com uma a seis pintas, haverá algo interessante a referir? Vamos desistir da impossibilidade de ocorrerem empates, mas acordamos que, quando num par de lançamentos houver um empate, ele é ignorado e o lançamento é repetido até à vitória de um dos lados.

Analisando a situação com um programa feito no Mathematica, foi possível recolher alguma informação: há 462 dados diferentes e com eles podemos construir 40666 ciclos não-transitivos. Mas 68 dados não intervêm nestes ciclos e, dos restantes 394, a frequência com que surgem é muito variável: desde dois dados ({1,1,2,2,2,4} e {3,5,5,5,6,6}) que aparecem, cada um, em apenas um ciclo, respetivamente {{1, 1, 1, 2, 4, 4}, {1, 1, 1, 3, 3, 4}, {1, 1, 2, 2, 2, 4}} e {{3, 3, 5, 6, 6, 6}, {3, 5, 5, 5, 6, 6}, {3, 4, 4, 6, 6, 6}}, até dois outros dados ({1,1,1,5,6,6} e {1,1,2,6,6,6}) que aparecem, cada um, em 1897 ciclos distintos.

⁴ Trybula e Steinhaus provaram que essa probabilidade mínima não pode exceder o valor encontrado naquele ciclo: 2/3. Ver [1] e [2].