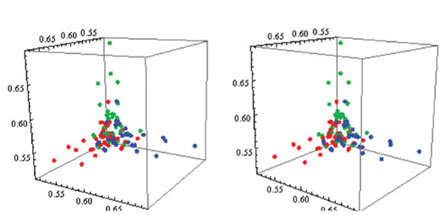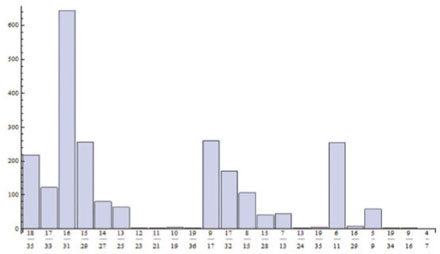
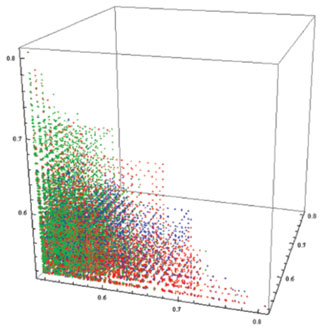
Fig 8	Fig 9	Fig 10
(clique na Figura 8 ou 9 para ver uma versão interactiva)

Os valores dos mínimos das probabilidades dos ciclos não-transitivos são {18/35, 17/33, 16/31, 15/29, 14/27, 13/25, 12/23, 11/21, 10/19, 19/36, 9/17, 17/32, 8/15, 15/28, 7/13, 13/24, 19/35, 6/11, 17/31, 16/29, 5/9, 19/34, 9/16, 17/30, 4/7, 15/26, 7/12} e oscilam, pois, entre 18/35 e 7/12, aparecendo com desigual frequência, como mostra o gráfico de barras (Figura 8).

Para se ter uma ideia, não só do mínimo das probabilidades para cada ciclo não-transitivo mas também do próprio terno das probabilidades (de cada dado ganhar ao seguinte), o melhor é fazer uma representação gráfica desses ternos. Note-se que, para cada ciclo, associar-lhe um terno de probabilidades pressupõe a escolha (arbitrária) de um elemento inicial do ciclo. As outras escolhas correspondem a rodar a figura anterior por ângulos de 120º e 240º, em torno da reta passando pela origem e com direção determinada pelo vetor (1,1,1). Esses três conjuntos de pontos estão representados a cores diferentes na Figura 9. E o par estereoscópico representa um conjunto análogo mas correspondente aos 3-ciclos de dados com apenas 1 a 4 pintas nas faces (Figura 10).