OPERAÇÃO – INVERSO

Quando dizemos que todo o número real a (não nulo) tem inverso para o produto usual estamos a afirmar a existência um número b que multiplicado (à esquerda ou à direita) nos dá o elemento neutro (e=1), ou seja, tal que a.b=b.a=1. E, no caso do produto habitual, sabemos que b=1/a.

No produto de caminhos (nas classes de homotopia) a verificação a fazer é análoga: ver que, dado um caminho, existe outro tal que multiplicado (à esquerda ou à direita) produz um caminho que é homotópico ao caminho constante.

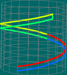
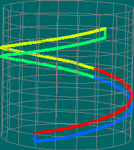
Mais formalmente, dado f de [0,1] em S, de A para A', existe f* de [0,1] em S tal que f.f* e f*.f são homotópicos a e e a e', respectivamente. Aqui f* é o caminho que percorre f em sentido contrário, ou seja, f* de [0,1] em S é dado por f*=f(1–t).

Tendo em conta a descrição da operação em caminhos percorridos durante uma hora, os produtos acima vão diferir no tempo e velocidades com que se percorre cada trilho.

No caso de f.f*:

Corresponde a percorrer f na primeira meia hora e f* na última. Isto significa, na primeira meia hora, percorrer f (com o dobro da velocidade) e na última meia hora voltar para trás (também com o dobro da velocidade), de regresso ao ponto inicial. Este produto é homotópico ao caminho e constante (igual ao valor inicial de f) e, formalmente, g1=f.f* de [0,1] em S pode ser definido por:
g1(t) = f(2t) se   0 t 0.5
f(2–2t) se   0.5 < t 1
 

No caso de f*.f:

Corresponde a percorrer f* na primeira meia hora e f na última. Isto significa, partir do ponto final de f e durante meia hora percorrer o caminho todo para trás (com o dobro da velocidade) e na última meia hora percorrer f com a orientação original (também com o dobro da velocidade), de regresso ao ponto final. Este produto é homotópico ao caminho e' constante (igual ao valor final de f) e, formalmente, g2=f*.f de [0,1] em S pode ser definida por:

g2(t) = f(1–2t) se   0 t 0.5
f(2t–1) se   0.5 < t 1
 

Portanto, os caminhos produto são diferentes de e e de e' ! No entanto, verifica-se que são todos homotópicos.

Formalmente, uma homotopia H de [0,1]x[0,1] em S (entre g1 e o caminho constante f(0)) pode ser dada por:

H(t,x) = f((1–x)2t) se   0 t 0.5 
f((1–x)(–2t+2)) se   0.5 < t 1 
(Clique sobre a figura para aceder ao applet.)

 

Descrição da operação
[Inverso]