OPERAÇÃO – ASSOCIATIVIDADE

Quando dizemos que o produto de números reais é associativo, estamos a referir-nos à propriedade (a.b).c=a.(b.c), ou seja, estamos a dizer que num produto de três elementos é indiferente começar por multiplicar os dois primeiros factores e depois multiplicar o resultado pelo último ou começar por multiplicar os dois últimos e depois multiplicar o primeiro por esse resultado.

Na associatividade do produto de caminhos (considerando as classes de homotopia) a verificação a fazer é análoga: ver que, dados três caminhos contíguos, o caminho que resulta do produto dos dois primeiros seguido do produto pelo terceiro é homotópico ao caminho que resulta do produto dos dois últimos a multiplicar pelo primeiro.

Mais formalmente, dados f1, f2 e f3 de [0,1] em S, tais que f1(1)=f2(0) e f2(1)=f3(0), (f1.f2).f3 é homotópico a f1.(f2.f3).

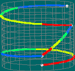
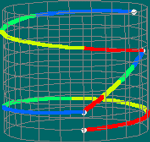
Tendo em conta a descrição da operação em caminhos percorridos durante uma hora, os produtos acima vão diferir no tempo e velocidades com que se percorre cada trilho.

No primeiro caso, (f1.f2).f3:  
O produto final é (f1.f2) por f3, ou seja, a primeira meia hora para (f1.f2) e última meia para f3; e como na primeira meia hora temos de percorrer dois caminhos, o primeiro quarto de hora fica para f1 e o segundo para f2. Ou seja, no primeiro quarto de hora é percorrido f1 (a uma velocidade quatro vezes maior que no caminho inicial), no segundo quarto de hora é percorrido f2 (também a uma velocidade quatro vezes maior) e na última meia hora é precorrido f3 (ao dobro da velocidade inicial).

Formalmente, g1=(f1.f2).f3 de [0,1] em S pode ser definida por:

g1(t) = f1(4t) se   0t0.25
f2(4t–1) se   0.25<t0.5
f3(2t–1) se   0.5<t1
No segundo caso, f1.(f2.f3):
  
O produto final é f1 por (f2.f3), ou seja, a primeira meia hora para f1 e última meia para (f2.f3); e como na última meia hora temos de percorrer dois caminhos, fica um quarto de hora para cada um deles. Ou seja, na primeira meia hora é percorrido f1 (ao dobro da velocidade inicial), no terceiro quarto de hora é percorrido f2 (a uma velocidade quatro vezes maior que no caminho inicial) e no último quarto de hora é precorrido f3 (também a uma velocidade quatro vezes maior).
Formalmente, g2= f1.(f2.f3) de [0,1] em S pode ser definida por:
g2(t) = f1(2t) se   0t0.5
f2(4t–2) se   0.5<t0.75
f3(4t–3) se   0.75<t1

Portanto, os caminhos produto são diferentes! Mas a associatividade verifica-se no conjunto das classes de homotopia, ou seja, mostra-se que os caminhos são homotópicos, bastando uma variação contínua das velocidades de percurso (ou da coloração dos elásticos).

Formalmente, uma homotopia H de [0,1]x[0,1] em S (entre g2 e g1) pode ser dada por:

H(t,x) =
f1( )
se  
f2(4t–2+x) se  
f3( )
se  
(Clique sobre a figura para aceder ao applet.)

 

Descrição da operação
[Associatividade]