| Atenção: |
|
esta
página, sempre que falarmos em recta e direcção,
estaremos a referir-nos a recta orientada e direcção
orientada (isto é, definida a partir de uma recta com
um sentido escolhido).
|
|
Este
problema consiste em, dado um corpo convexo
e limitado no plano, encontrar o menor número de direcções
(diferentes), no plano deste conjunto, de modo a que cada um dos pontos
da fronteira do conjunto seja 'iluminado' por alguma dessas direcções.
|
Só para ficar com uma ideia: Imagine que tem um corpo opaco plano pousado numa mesa e que quer iluminar-lhe a fronteira (a linha exterior) com o mínimo de direcções de luz possíveis, direcções essas pousadas na mesa. Um ponto só é iluminado por uma certa direcção de luz se houver uma recta com essa direcção que incida no ponto directamente (isto é, que não passe 'de raspão') e que incida de fora para dentro do corpo (isto é, o ponto iluminado é o primeiro ponto em que dá a luz).
Sendo um pouco mais rigorosos: Um ponto A da fronteira de um corpo convexo F é ponto de iluminação relativamente à direcção l se o feixe de raios paralelos com direcção l ilumina o ponto A na fronteira de F e também uma vizinhança de A nessa fronteira.
Ou ainda: O ponto A da fronteira de um corpo convexo F é ponto de iluminação relativamente à direcção l se satisfaz:
2. A é o primeiro ponto de F que se encontra avançando ao longo de r na direcção l.
 |
 |
|
|
Nesta
figura o ponto A é iluminado pela direcção l.
|
Nesta
figura os pontos A e V não são iluminados pela direcção
l pois a recta paralela a l que passa pelos pontos é
uma recta
de suporte de
F.
|
As direcções l1, l2, l3, ... , ln são suficientes para iluminar a fronteira de F, se cada ponto da fronteira é ponto de iluminação relativamente a pelo menos uma destas direcções.
Vou chamar c(F)
ao menor número de direcções (no plano de F) suficientes
para iluminar toda a fronteira de F.
|
Por
exemplo, para um círculo bastam 3 direcções para
iluminar toda a sua fronteira:
|
 |
||||||
|
Para iluminar
toda a fronteira de um paralelogramo já não chegam 3 direcções;
precisamos de 4 direcções:
|
 |
Pode-se experimentar este resultado no sketch seguinte. A figura F, de momento, é um triângulo e está a ser iluminada por três direcções. Temos portanto que c(F) é menor ou igual a 3. Todos os pontos a vermelho podem ser movidos; pode-se assim alterar as direcções da luz, no canto superior esquerdo, para ver que pontos da fronteira do triângulo são iluminados. Pode-se também mover os vértices do triângulo para transformar a figura F num quadrilátero qualquer, que (desde que não seja um paralelogramo) também necessita de apenas 3 direcções para ser iluminado: é só procurar direcções de luz adequadas. Atenção, que estamos a supor que a figura é convexa.
(O applet seguinte foi produzido
com o auxílio do JavaSketchpad)
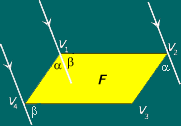
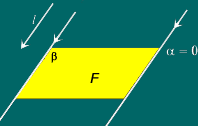
Por que é que, se F ficar um paralelogramo,
as três direcções não são suficientes para
iluminar toda a fronteira?
Porque temos quatro vértices e quatro lados paralelos dois a dois.
Para iluminar estes 4 vértices com 3 direcções teria
de haver pelo menos uma direcção que iluminasse dois vértices
e isso não é possível. Para iluminar um vértice
V1 precisamos de uma direcção de luz tal que uma recta paralela
a essa que passa por V1 intersecte o interior do paralelogramo, logo tem de
ser uma direcção de luz com um ângulo entre os ângulos
dos dois lados do paralelogramo (como se vê nas figuras, a e b têm
de ser maiores que zero, pois se a=0 ou b=0 formam-se rectas de suporte que
não iluminam os vértices). Ao tentar iluminar o vértice
adjacente V2 (ou V4) com essa mesma direcção, a recta paralela
que passa por V2 (ou V4) já não contém pontos do interior
do conjunto, logo não ilumina o vértice V2 (nem V4).
 |
 |
.gif){kind=small}
|
|
Cobertura por conjuntos homotéticos |