Dado um conjunto F, queremos encontrar uma partição desse conjunto F, de modo a que cada parte tenha diâmetro menor que o diâmetro de F, e de modo a que o número de partes em que o conjunto F fica dividido seja o mínimo possível.

Estamos a habituados apenas a falar em diâmetro de um círculo ou de uma esfera, mas também podemos falar em diâmetro de qualquer outro conjunto limitado e não vazio, se definirmos diâmetro como o supremo das distâncias entre dois pontos quaisquer desse conjunto. Nesse caso, temos, por exemplo, que o diâmetro de um quadrado é o comprimento de uma das suas diagonais e o diâmetro de um triângulo equilátero é o comprimento de um dos seus lados:
 

Diâmetros de alguns conjuntos no plano

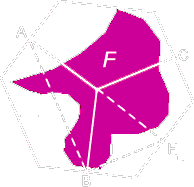
Por exemplo, se partirmos um círculo com diâmetro d em duas partes, pelo menos uma delas tem diâmetro d. No entanto, existe pelo menos uma maneira de o partir de forma a que cada parte tenha diâmetro menor que d. A figura seguinte exemplifica uma dessas partições:

O número de Borsuk de um círculo é 3.

Tanto um rectângulo como uma elipse, ou ainda um segmento de recta, têm número de Borsuk igual a 2.

Há bastantes conjuntos com número de Borsuk menor que 3. Mas será que há algum conjunto no plano que tenha número de Borsuk maior que 3?

A resposta é NÃO,: qualquer que seja o conjunto limitado no plano que escolhermos, esse conjunto pode ser partido em 3 partes com menor diâmetro, logo o seu número de Borsuk é no máximo 3.
 

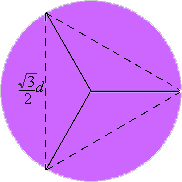
Suponhamos que estamos a considerar um subconjunto F do plano com diâmetro d. Consideremos um hexágono regular, com distância d entre os seus lados opostos, e que contenha o nosso conjunto F. (Acreditem que um tal hexágono realmente existe!) Partindo esse hexágono em três partes com diâmetro menor que d, obtemos uma partição de F em 3 partes com diâmetro menor que d. Uma tal partição do hexágono é a que se vê na figura ao lado, onde temos as 3 partes do hexágono, cada parte com diâmetro menor que d, pois o triângulo ABH (onde A,B,H são os pontos médios dos lados a que pertencem) é rectângulo em B, sendo o diâmetro de cada parte do hexágono igual a AB<AH=d. Logo cada uma das partes em que F é partido também tem diâmetro menor que d.

	Um elipsóide alongado E tem número de Borsuk igual a 2.
	Um cone C, com altura menor que o diâmetro da base, tem número de Borsuk igual a 3.

E qual será o número de Borsuk de uma bola tridimensional?

Não é possível partir uma bola em duas partes com menor diâmetro...

.. e não é possível partir uma bola em três partes com menor diâmetro...

...mas é possível fazê-lo usando quatro partes!

Como?

 

Cortando uma calote polar com altura menor que o raio da esfera e depois dividindo o restante em 3 gomos iguais:   ou       Inscrevendo na bola um tetraedro regular de faces T1, T2, T3 e T4 e considerando os cones K1, K2, K3 e K4, que são a união de todos os raios com origem no centro da bola e que passam por algum ponto da face T1, T2, T3 ou T4 respectivamente. As partes constituidas por cada um destes cones K1, K2, K3 e K4 formam uma partição da bola onde cada parte tem menor diâmetro:

A resposta também é NÃO. Todos os corpos limitados tridimensionais têm número de Borsuk no máximo 4. A prova deste resultado recorre a um lema que diz que qualquer conjunto tridimensional com diâmetro d está contido num octaedro recto cujas faces opostas estão à distância d umas das outras e com três dos seus vértices cortados por planos ortogonais às diagonais e que distam do centro d/2.
 

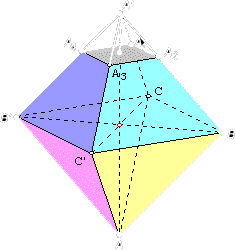
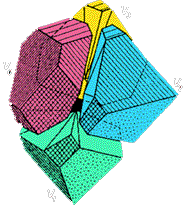
O corpo F está contido num octaedro recto ABCA'B'C'...	...ao qual foram cortados 3 dos seus vértices por planos ortogonais às diagonais e que distam do centro d/2...

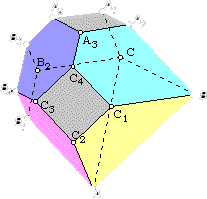
...e que pode ser partido em 4 partes com diâmetro menor que d, partindo assim F em 4 partes de menor diâmetro.

Já vimos o que acontece ao número de Borsuk para conjuntos no plano e no espaço tridimensional. E que números de Borsuk poderemos ter para conjuntos em espaços de maior dimensão?

De um modo análogo ao que vimos em cima para uma bola tridimensional, se pode ver que uma bola n-dimensional tem número de Borsuk igual a n+1. Será que, tal como acontece no plano e no espaço tridimensional, a bola n-dimensional (n>2) tem o maior dos números de Borsuk possíveis para os conjuntos de dimensão n?

Houve quem pensasse que SIM, que tal como em dimensão 2 e 3 o número de Borsuk máximo é o do círculo e o da bola, respectivamente, em dimensão n (mais elevada) o número de Borsuk máximo seria o da bola n-dimensional.

O matemático que estudou inicialmente estas questões, K. Borsuk, fez em 1933 a seguinte conjectura:

http://www.ams.org/journals/bull/pre-1996-data/199329-1/Kalai

A conjectura de Borsuk afinal não era válida, pois Kahn e Kalai mostraram que em espaços de elevada dimensão é possível construir um contra-exemplo, e até mostraram que o número de Borsuk cresce exponencialmente quando a dimensão tende para o infinito.

Durante o tempo em que se tentava provar a conjectura de Borsuk, foram-se encontrando outros majorantes para os números de Borsuk possíveis em espaços de dimensão n, numa tentativa de obter finalmente o majorante conjecturado.

Em 1955, usando partições de cubos n-dimensionais, H. Lenz provou que para qualquer corpo n-dimensional F se tem a(F)<(sqr(n)+1)ⁿ. Este valor afasta-se bastante do valor conjecturado por Borsuk, pois, por exemplo para n=4, apenas garante a possibilidade de qualquer corpo ser partido em 81 partes de menor diâmetro.

Em 1982, usando partições de bolas n-dimensionais, Lassak provou que para qualquer corpo n-dimensional F se tem a(F)< 2^{n -1}+1, o que, para n=4, já garante a possibilidade de qualquer corpo ser partido em 9 partes de menor diâmetro.
 

Voltar atrás

Cobertura por conjuntos homotéticos

Problema da Iluminação