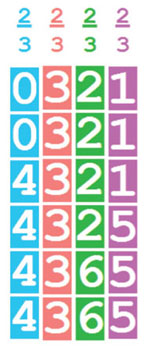
 Fig 4 |
O quadro ao lado representa bem o ciclo de dados que se considerou: em cada coluna estão indicados os números de pintas das seis faces e em cima a probabilidade de esse dado ganhar ao representado na coluna seguinte (a seguinte à última é a primeira). Na situação atrás referida, se, realmente, o primeiro jogador tivesse escolhido o dado A, bastaria ao segundo escolher D, para ter uma probabilidade de 2 contra 1 de ganhar ao primeiro. Mas se o primeiro jogador tivesse escolhido qualquer outro dado, bastaria ao segundo escolher o precedente (na seriação A, B, C, D) para ter uma probabilidade de 2 contra 1 de ganhar ao primeiro. Isto é, o jogador que escolhe o dado em segundo lugar é que parte em grande vantagem, pois pode sempre escolher um dado melhor do que o do outro jogador (a noção de cortesia é invertida neste contexto: ser cortês é aqui “servir-se primeiro” e não “deixar o adversário servir-se”...). Conclusão: a pergunta inicial está mal formulada e induz uma ideia errada; antes de perguntar qual o dado melhor, seria prudente estar certo de que existe sempre um dado melhor do que todos os restantes (pelo menos num sentido lato). Ora isso não acontece, como o comprova o exemplo dado. Na exposição “Matemática Viva”, havia uma mesa (ver foto da figura 1) e, sobre ela, quatro dados com a composição A, B, C, D indicada acima. Com quatro jogadores à volta da mesa, cada um jogava um número razoável de vezes com o seu vizinho da direita e anotava o resultado, depois o da direita jogava com o seguinte (à direita) e assim sucessivamente. Com grande probabilidade2, cada jogador ganhava ao jogador à sua direita, o que acabava por “sugerir” que não havia nenhum dado melhor do que todos os outros3. |
2 Suponhamos
que, para cada par de jogadores, há um lançamento dos
dois dados, não apenas uma vez, mas sim um número n (ímpar)
de vezes. Se se considerar ganhador aquele que mais vezes obtiver um
número maior do que o do oponente, então a probabilidade
de A ganhar a B neste jogo aumenta relativamente à de A ganhar
a B com apenas um lançamento de A e outro de B (suposta >
0.5). É esta a razão pela qual se preconizava no módulo
da “Matemática Viva” que os visitantes repetissem
várias vezes os lançamentos. O leitor pode verificar que
essa probabilidade é dada pela seguinte fórmula:
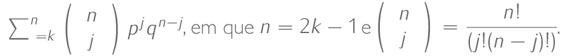
Os primeiros vinte valores, para n = 1,3,...,39 são aproximadamente:
0.667, 0.741, 0.790, 0.827, 0.855, 0.878, 0.896, 0.912, 0.925, 0.935,
0.944, 0.952, 0.958, 0.964, 0.969, 0.973, 0.977, 0.980, 0.982, 0.984.
3 Refira-se como curiosidade que, se B jogasse com D, a probabilidade de lhe ganhar seria 1/2, e, se A jogasse com C, a probabilidade de A ganhar seria 4/9.