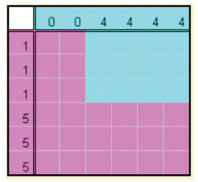
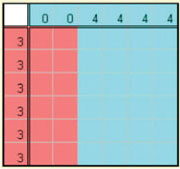
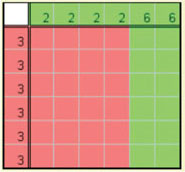
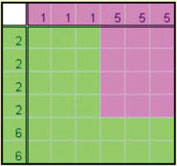
Suponhamos agora que A tem duas faces sem pintas e quatro com 4 pintas, o que convencionamos descrever por A = (0, 0, 4, 4, 4, 4) e, com notação análoga, suponhamos B = (3, 3, 3, 3, 3, 3). Em cada par de lançamentos (de A seguido de B) o jogo nunca empata, e há 36 pares (igualmente prováveis) de faces possíveis (em cada par de lançamentos), mas os pares de números obtidos são apenas dois: (0, 3), em que ganha B e (4, 3), em que ganha A. Ora, dos 36 casos possíveis, 12 correspondem a (0, 3) e 24 a (4, 3). Portanto, a probabilidade de B ganhar é 12/36 = 1/3 e a de A ganhar é o dobro: 24/36 = 2/3. Se B jogar com um terceiro dado C = (2, 2, 2, 2, 6, 6), também nunca há empate, B ganha a C em 24 dos 36 casos e C ganha a B nos outros 12: podemos traduzir a situação, dizendo que B é duas vezes melhor do que C. Deixamos ao leitor a verificação de que, tomando como quarto dado D = (1, 1, 1, 5, 5, 5), C é duas vezes melhor do que D. (Para controlar ou evitar as contas, pode usar uma calculadora de probabilidades).

Fig 2

Chegados a este ponto, e encarando apenas as observações feitas, parece que, relativamente à questão formulada no início do artigo, é natural conjeturar que, no caso dos dados A, B, C, D acima definidos, a resposta é clara: o dado A é o melhor dos quatro, uma vez que é melhor do que B, este é melhor do que C e C é melhor do que D. Em particular, se dois jogadores decidirem jogar e, antes de começarem, tiverem a oportunidade de escolher o dado que preferem (entre A, B, C e D), parece que o primeiro parte em vantagem, bastando-lhe escolher o dado A.