Para determinarmos o que é o conjunto dos pontos correspondentes às chaves de um jogo de totobola com 4 partidas temos de estudar o problema na 4ª dimensão e descobrir o que é um cubo nessa dimensão.

Comecemos por analisar a situação usual:

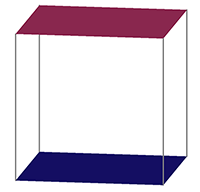
• um cubo, de dimensão 3, é constituído pelas seguintes partes: o seu interior (de dimensão 3), as faces (de dimensão 2), as arestas (de dimensão 1) e os vértices (de dimensão 0);
• as partes de um quadrado são: o seu interior (de dimensão 2), as arestas (de dimensão 1) e os vértices (de dimensão 0).

Assim:

• um quadrado pode ser visto como um cubo de dimensão 2, 2-cubo;
• um segmento pode ser visto como um cubo de dimensão 1, 1-cubo;
• um vértice corresponde a um cubo de dimensão nula, 0-cubo.

Por analogia, um cubo de dimensão 4, 4-cubo, usualmente conhecido por hipercubo, é constituído por: o seu interior (de dimensão 4), as faces cúbicas (de dimensão 3), as faces quadradas (de dimensão 2), as arestas (de dimensão 1) e os vértices (de dimensão 0).

Generalizando, podemos obter um cubo de dimensão n, um n-cubo.

Um quadrado (2-cubo) pode ser construído unindo dois segmentos-de-recta (1-cubos) paralelos.

Um cubo (3-cubo) pode ser construído unindo dois quadrados (2-cubos) paralelos.

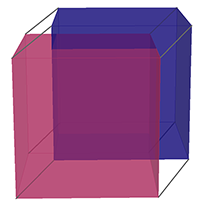
Um hipercubo (4-cubo) pode ser construído unindo dois cubos (3-cubos) paralelos. [2]