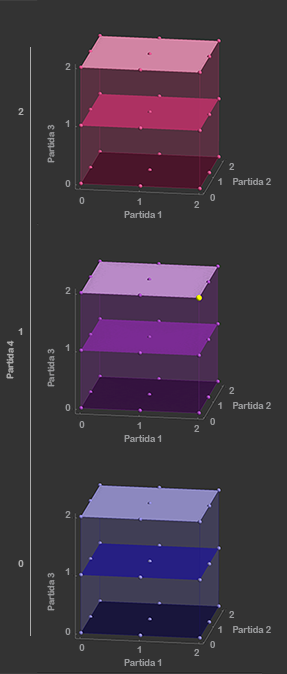
Para estudarmos o problema de saber qual o número mínimo de apostas que garante pelo menos o 2º prémio em jogos de totobola com 4 partidas ou mais, de um ponto de vista geométrico, temos de “mergulhar” em espaços de dimensão superior a 3.

Para um jogo de totobola com 4 partidas, o número de apostas possíveis é \(3^{4}=81\) , pois existem 3 possibilidades (1, X ou 2) para cada partida. Quando o totobola é constituído por apenas 2 partidas, o conjunto das 9 chaves é o conjunto dos vértices, pontos médios e centro de um quadrado (de dimensão 2). Para um jogo de totobola com 3 partidas, o conjunto das 27 chaves é o conjunto dos vértices, pontos médios das arestas, centros das faces e centro de um cubo (de dimensão 3).

E para um jogo de totobola com 4 partidas, o que é o conjunto das 81 chaves possíveis? De forma análoga ao que foi feito para 2 e 3 partidas, se substituirmos os símbolos do totobola 1 X 2 por 0 1 2, respectivamente, obtemos para cada chave 4 coordenadas, que irão corresponder a um ponto da 4ª dimensão. Por exemplo, a chave 2-1-2-X corresponde ao ponto de coordenadas (2,0,2,1).

Representações no espaço e no plano dos pontos com 4 coordenadas correspondentes às 81 chaves de um jogo com 4 partidas. A amarelo encontra-se assinalado o ponto de coordenadas (2,0,2,1): 2 na Partida 1; 0 na Partida 2; 2 na Partida 3 e 1 na Partida 4. Note-se que a última coordenada indica em que cubo estará o ponto.