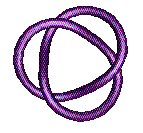TORUS KNOTS
(Page 2 of 2)
The (5,4) torus knot was used by John Robinson




as the initial idea for
ORACLE , which is a stretched
out version of the knot. In the picture of the (5,4) torus knot you
will see many crossings. How many?
It was proved by Murasugi in 1991, that if p, q
are coprime numbers with |p|>|<|q|q| then
the (p,q) torus knot has a crossing
number |p|(|q| -1), i.e it has a diagram with this number of
crossings, and this number is minimal. Also Kronheimer and Mrowka proved in
1993 that the unknotting
number of T(p,q) is (|p|-1)(|q|-1)/2
.
Torus knot T(p,q) with small p,
q can be pretty. Here is the trefoil T(3,2)
and also its mirror
image T(3,-2).
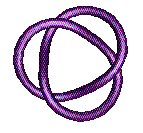

The Trefoil .....and its Mirror Image
When the trefoil T(3,2) has the Torus added in,
it can look very effective, by changing round the thickness of the torus
and the knot. How difficult would this be to build with a ribbon and ring
in the real world ?



Don't you think the ribbon would keep falling off and taking short cuts?
It would take a great deal of sticky tape and patience to create the same
picture!
There is another trefoil, the T(2,3).


It doesn't really look like the same knot though does it! However, if you
made a replica out of string (with the ends tied of course) and fiddled enough,
you should be able to prove it's the same! This picture shows the trefoil
as a 2-bridge
knot.
Even unknotted forms, such as T(1,3) are attractive





and indeed this gives the edge of
ETERNITY .
We have also discovered a page describing how to construct Maple plots of
Torus Knots at
The Geometry Center (outside link), University
of Minnesota.
MATHEMATICAL THEMES
-
Borromean Rings - what
they are and why they don't exist!
-
The Möbius Band - what
one looks like, experiments to try, and a beautiful rotating golden one enabling
you to really see what one looks like in 3D (this is optional as 90Kb).
-
Bernard Morin and the Brehm Model
- how Bernard Morin showed John Robinson the Brehm Model of the
Möbius Band and how to make one!
-
The Projective Plane -
how to create and understand the projective plane when it is not possible
to physically construct (this relates to the Brehm Model in the Projective
Plane). Also the Dirac String Trick.
-
Fibre Bundles - what
they are, how to make them, and examples of them in John Robinson's Work.
-
Knots and Links -
Introduction to the subject of Knot Theory, includes history of the subject,
and a rotating mathematically constructed Immortality (the trefoil being
one of the most basic knots).
-
Fractals 3 pages, introducing
Fractals, considering iteration, The Sierpinski Gasket and the applications
of the subject.
-
Exhibition
"Mathematics and Knots"
-
Ronnie
Brown's Homepage
-
John Robinson's Symbolic
Sculpture
-
Brochure
(140Kb), giving a guided Tour around the Symbolic Sculptures at the
University of Wales, Bangor.
- About the Centre
for the Popularisation of Mathematics
©Mathematics and
Knots/Edition Limitee 1996
This material may be used freely for educational, artistic and scientific
purposes, but may not be used for commercial purposes, for profit or in texts
without the permission of the publishers.