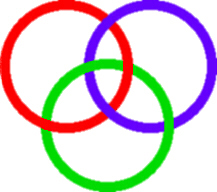

As you can see, it consists of three circles, linked so that they cannot be pulled apart. But no individual circle links with any one other, it is only the figure as a whole which cannot be disentangled.
This is an example of what mathematicians call a `link with three strands' . The study of such links is part of Knot Theory, a mathematical topic which studies the form of knots and links. At the present time it does not study some matters of interest to a practical user such as the size of the knot when made up of string or rope, or its suitability as a knot for a particular and practical task. Nonetheless, the theory has amazing relations with topics such as polymer theory and theoretical physics. For more information try looking at the Knot Plot Site (outside link).
If you try and make the Borromean Rings out of wire, you will find that you cannot make real flat circles into the figure. There must always be kinks.
The Maple Picture below is a very good example of these kinks; it was created by I.J.Mcgee, by inputting the Code underneath it.
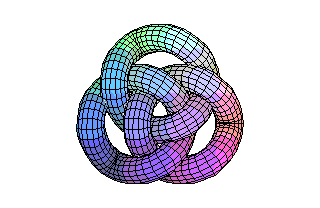
with(plots):
r:=sqrt(3)/3:
specs:=t=0..2*Pi,radius=0.3,tubepoints=17,numpoints=50:
c1:=[cos(t),sin(t)+r,-cos(3*t)/3,specs]:
c2:=[cos(t)=1/2,sin(t)-r/2,-cos(3*t)/3,specs]:
c3:=[cos(t)-1/2,sin(t)-r/2,-cos(3*t)/3,specs]:
specs1:=orientation=[-90,0],style=PATCH,scaling=CONSTRAINED:
tubeplot({c.(1..3)},specs1);
The picture is produced using a tube plot in Maple, that is it follows the line of a curve, creating a tube of circular cross-section. It must have taken quite some time to get the parameterisation correct!
The theorem stating Borromean rings to be impossible with flat circles is proved rigorously in the article "Borromean circles are impossible," Amer. Math. Monthly, 98 (1991) 340-341, by B.Lindström and H.-O. Zetterström..
There is another proof (outside link) that flat Borromean circles do not exist, using hyperbolic geometry in four dimensions.
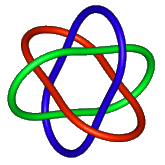
|
It is however possible to produce it with ellipses. There are many examples of this in not Knot (outside link). |
John Robinson found that if you use squares instead of circles then
you can make a real figure. Try it yourself with cardboard cutouts.
It was also surprising that the form lifted into an extraordinary shape as
shown in CREATION. You will be interested
to find that if the shape is made out of card correctly then it also folds
flat. So you can make yourself a travelling sculpture!
If you like geometry and trigonometry, then you can try and calculate the various distances between the corners and angles between the parts. Successful solutions could be advertised here!
John then experimented with other forms, and the results were GENESIS, and INTUITION. His experiments as a sculptor and true geometer have inspired mathematicians to explore these forms.