Consideremos um pentágono inicial cujas abcissas dos vértices são x₀, x₁, x₂, x₃ e x₄. Para cada x_r, vamos escrever

Temos assim um sistema de 5 equações com 5 incógnitas: X, P₁, Q₁, P₂ e Q₂. Este sistema é possível e determinado, pelo que, sabendo o valor das abcissas, podemos calcular o valor das incógnitas. Por exemplo, para calcular o valor de X basta ver que, somando as cinco equações obtém-se

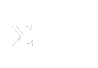
ou seja,

e X representa a abcissa do centro de gravidade dos 5 vértices. Notemos agora que, escrevendo o vector (P₁,Q₁) na forma polar , temos

Analogamente, temos

pelo que

Então, vem

De seguida, temos

e, mais geralmente,

Quando k tende para infinito, as parcelas e tendem ambas para zero. No entanto, a segunda parcela tende mais rapidamente para zero do que a primeira, pelo que podemos desprezá-la e fazer a seguinte aproximação:

para um valor de k elevado. Fazendo e , vem

ou seja,

onde e . Analogamente, temos

e, considerando pontos no espaço,

Temos então que os pontos aproximam-se cada vez mais do plano (eventualmente degenerado) definido pelo ponto (X,Y,Z) e pelos vectores (P,R,T) e (Q,S,U). Este plano não depende de k, podendo ser determinado a partir do pentágono original.

Seja f a aplicação linear cuja matriz é . Temos então que , sendo que os pontos são os vértices de um pentágono regular inscrito numa circunferência de raio unitário e centrada na origem. Assim, os pontos aproximam-se cada vez mais dos vértices do pentágono que se obtém aplicando a função f a esse pentágono regular, seguida de uma translação segundo o vector (X,Y,Z). Assim, enquanto que o pentágono regular estava inscrito numa circunferência de raio unitário e centrada na origem, este pentágono encontra-se inscrito numa elipse centrada em (X,Y,Z), e os segmentos que eram paralelos no pentágono regular (cada lado é paralelo a uma diagonal) continuam a ser paralelos neste pentágono, como pode ser observado na figura abaixo

Cada lado do pentágono inscrito na elipse é paralelo a uma das suas diagonais.

Notemos também que

Mas, como

vem

Assim, os pontos que se obtêm aplicando duas vezes o processo de bissecção a um pentágono são, aproximadamente, os mesmos pontos que se obtêm por uma homotetia de centro no centro de gravidade desse pentágono e de razão , sendo a aproximação tanto melhor quanto maior for o valor de k. Isto explica o facto de, na sucessão de pentágonos obtida, estes parecerem surgir alternadamente com a mesma forma, apenas com um tamanho menor.