 ,
obtivémos um novo polígono de n
lados cujas abcissas dos vértices são dadas, para certos valores fixos
,
obtivémos um novo polígono de n
lados cujas abcissas dos vértices são dadas, para certos valores fixos
 ,
por
,
porGeneralização
Notemos que, em todos os
processos de construção considerados anteriormente, a partir de um
polígono inicial de n
lados cujas abcissas dos vértices são xj,
com  ,
obtivémos um novo polígono de n
lados cujas abcissas dos vértices são dadas, para certos valores fixos
,
obtivémos um novo polígono de n
lados cujas abcissas dos vértices são dadas, para certos valores fixos
 ,
por
,
por
 |
Vejamos alguns exemplos:
1. Se
e
para j > 1, então temos
, onde xn = x0.
2. Se
,
e
para j > 1, então temos
, onde xn = x0.
3. Se, para algum p entre 0 e 1,
,
e
para j > 1, então temos
, onde xn = x0.
4. Se
e
para
, então temos
, onde xn = x0 e x-1 = xn-1.
Assim, dado  ,
temos
,
temos
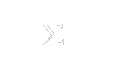
onde  para todo
para todo  .
.
Se considerarmos, para
cada inteiro positivo k,
 ,
então vem
,
então vem

onde  e
e  .
.
Equivalentemente, temos

Deste modo, recorrendo a conhecimentos de Álgebra Linear, podemos tirar conclusões sobre as sucessões de polígonos que temos vindo a considerar. De facto, demonstra-se que a matriz A tem n valores próprios complexos (não necessariamente distintos), dados por
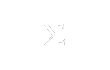
para todo  ,
sendo
,
sendo  uma raiz primitiva de ordem n
da unidade. Para saber mais, consulte este
documento (em formato PDF).
uma raiz primitiva de ordem n
da unidade. Para saber mais, consulte este
documento (em formato PDF).
De que forma podemos aplicar o que vimos aos exemplos dados anteriormente?