À volta da roda

Num veículo de quatro rodas circulares, cada par delas está unido por um eixo que passa pelos centros das rodas. O formato da roda garante que todos os pontos do seu bordo estão à mesma distância do seu centro, pelo que o eixo se desloca sem oscilações. Mas, se pretendermos transportar um objecto pesado, o sistema de rodas unidas por um eixo pode não ser suficientemente robusto e, por isso, é frequente utilizarem-se rolos: os objectos são transportados numa plataforma que rola sobre cilindros de igual secção. Também deste modo o transporte decorre sem oscilações, mas agora a propriedade responsável por este movimento suave é o facto de a circunferência ter largura constante. A diferença essencial é que no primeiro caso (carros usuais) a estrutura do carro apoia-se nos eixos, enquanto no segundo se apoia nos bordos das rodas (ou rolos).

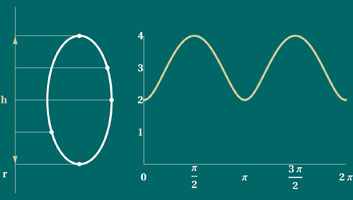
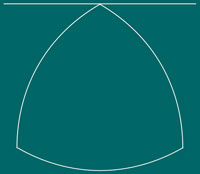
Por exemplo, uma circunferência de diâmetro d tem largura constante d. Mas esta não é uma propriedade que a caracterize pois há infinitas outras curvas que a satisfazem. A mais simples é o triângulo de Reuleaux, que se obtém, a partir de um triângulo equilátero de lado L, se desenharmos três arcos de circunferência com raio L e centro em cada um dos vértices do triângulo. Verifiquemos que a curva assim obtida tem largura constante L.