O TEOREMA FUNDAMENTAL DAS CURVAS

No caso planar existe ainda uma outra definição de curvatura (com sinal). Neste caso, tem-se que uma curva plana é determinada, a menos de um movimento euclidiano, pela sua curvatura com sinal. Este facto, leva-nos à conjectura de que uma curva espacial é determinada, a menos de um movimento euclidiano, pela sua curvatura e pela sua torção. De facto, tal é verdade mas temos de incluir uma condição suplementar (essencial para garantir a unicidade).

 

TEOREMA FUNDAMENTAL DAS CURVAS (T. F. Curvas):

Seja P₀ um ponto de ³ e TF₀ um triedro ortonormado definido positivamente. Sejam k, : I³ duas funções contínuas, com k > 0 em I.

Então, existe uma e uma só curva C², c: I ³, parametrizada pelo comprimento de arco, cuja função curvatura é k, cuja função torção é , cujo ponto inicial é P₀ e cujo Triedro de Frenet inicial é TF₀.

(Ver, por exemplo: M. Spivak, A comprehensive introduction to differential geometry (vol. 2); 1999)

 

Observação: O pressuposto de que a curvatura é sempre maior que zero é essencial para garantir a unicidade da curva. Com efeito:

(1) Consideremos as seguintes funções em ³:

f ( t ) = ( t ³, t , 0 );

g ( t ) =		( t 3, t , 0 ),	se t < 0	.
		( 0 , t , t 3),	se t 0

As duas funções têm a mesma função curvatura e esta anula-se em t = 0. A torção em ambos os casos é sempre nula nos pontos onde esta está definida (todos os pontos, com excepção do instante zero). Os pontos iniciais e os Triedros de Frenet iniciais também são os mesmos nas duas curvas (note-se que as curvas são coincidentes até ao instante t = 0). Mas não há nenhum movimento euclidiano que possa levar uma das curvas na outra, como se pode ver na figura seguinte:

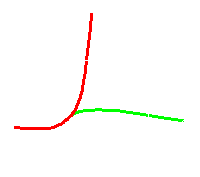
(2) Um outro exemplo semelhante ao anterior pode ser dado pelas funções:

f ( t ) = ( 0 , 0 , 0 ), se t = 0 ; ( t , 0 , 5 Exp( - t -2 ) ), se t 0

g ( t ) = ( t , 5 Exp( - t -2 ) , 0 ), se t < 0 . ( 0 , 0 , 0 ), se t = 0 ( t , 0 , 5 Exp( - t -2 ) ), se t > 0

 

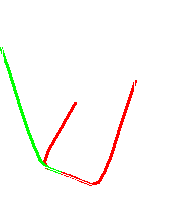
(A. Gray, Modern Geometry of Curves and Surfaces, pp. 142-145)

Este tipo de exemplos justifica a opção de não se considerar que a torção seja zero quando a curvatura é nula. Com a opção tomada, continua a ser válido que uma curva tem torção nula num intervalo se e só se a curva for planar nesse mesmo intervalo. Repare que se a torção fosse zero nos pontos onde a curvatura se anula, tal já não seria verdadeiro (ver, por exemplo, as funções g apresentadas acima)

voltar