A FUNÇÃO CURVATURA ( no caso planar)

Seja  f: I² uma curva parametrizada diferenciável. Para cada t I onde f´(t) 0, fica definida uma única recta na direcção de f´(t), que é denominada de tangente em t. No estudo das curvas é conveniente assumir a existência de tangente em todos os pontos da curva e portanto surge a seguinte definição:

Definição: Uma curva parametrizada diferenciável  f: I² é dita regular se f´(t) 0 para todo o t I.

O comprimento de arco de uma curva parametrizada regular  f: I², a partir do ponto t₀ I, é por definição

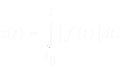
Tem-se ainda que s´(t) = I f´(t) I.

Diz-se que uma curva parametrizada regular está parametrizada pelo comprimento de arco se I f´(t) I = 1 para todo t I.

Supondo que a curva f determina a posição de uma determinada partícula, a curva está parametrizada pelo comprimento de arco precisamente quando a partícula se move com velocidade constante igual a 1.

A definição de curvatura que se irá apresentar a seguir apenas é válida para curvas parametrizadas pelo comprimento de arco. Esta restrição não é muito grande, uma vez que é possível, dada uma qualquer curva suave, determinar uma curva diferenciável, parametrizada pelo comprimento de arco, que tenha o mesmo traço que a curva inicial.

Diz-se ainda que T = ( T₁, T₂ ) é o vector tangente e que N = ( N₁, N₂ ) é o vector normal à curva num determinado ponto. A tangente é dada por f´(t) enquanto que o vector normal é dado por

Definição: Seja   f: I² uma curva parametrizada pelo comprimento de arco s I. A função curvatura (com sinal) de f é dada por

k ( s ) = § . I f´´(s) I

onde § é definido do seguinte modo

Valor de §	Condição	"Esquema"
§ = 1	T1 x N2 - T2 x N1 > 0
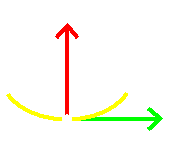§ = -1	T1 x N2 - T2 x N1 < 0

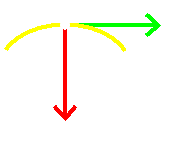voltar