Voltemos a observar a concha, mas
agora encarando-a como um objecto de 
3
(ou seja, como um objecto tridimensional).
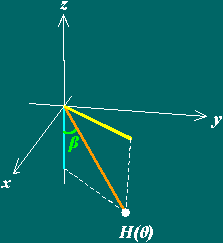
Pretendemos agora encontrar uma curva que "vista de cima" seja semelhante a uma espiral equiangular mas que vá "descendo continuamente" em relação ao plano horizontal que contém o ponto inicial da curva. Uma curva com tal propriedade designa-se por helicoidal.
Para aproveitar a equação
que temos no caso planar, suponhamos que a "passagem" da espiral
para a helicoidal, H(
),
não altera a distância entre os pontos e a origem do referencial,
ou seja,
continua a representar a distância do respectivo ponto da curva à origem.
(clique na figura para abrir o applet respectivo)
 =
r() 
|
 |
= r()
cos ( )
|
|
= r()
sin () |
|||
Então, a cota desta curva será dada por
onde
(0º 
90º) é o ângulo de alargamento da helicoidal.
Por outro lado, observemos que para obter as equações x() e y() desta helicoidal basta substituir r() por
nas equações indicadas para a espiral.
Para observar o
que acontece à helicoidal quando se variam os parâmetros 
,
e A,
veja o seguinte applet.
Em resumo, em coordenadas
cartesianas a equação da helicoidal pretendida, H()
= (x(),
y()),
é dada por
|
 |
. |
 |
||
 |
Já temos o modelo matemático para os "alicerces" da concha. Falta-nos ainda o modelo para as paredes...