Em primeiro lugar, observemos uma concha, como a da figura seguinte, vista de perfil e estudemos a sua forma (olhando-a como se fosse um objecto bidimensional).
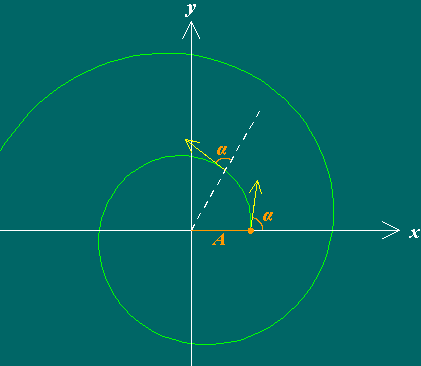
A curva que melhor se aproxima desta forma é a espiral equiangular (também conhecida por espiral logarítmica) que, em coordenadas polares, tem equação
onde
= 0);
(0º <
< 90º) é o ângulo de abertura da espiral.Para observar o que
acontece à espiral quando se variam os parâmetros
e A, veja
o seguinte applet.
Observações:
(a)
r(0)
indica a distância do ponto da curva em 0
à origem do referencial;
(b)
O caso
= 90º gera uma circunferência, o que não seria bom
para o seu habitante pois este, ao crescer, acabaria por ficar preso dentro
da própria concha; o caso
= 0º gera uma linha recta o que não tornaria a concha um
bom esconderijo para o seu habitante.
Em coordenadas cartesianas,
esta espiral, h()
= (x(),
y()),
é definida por
 |
 |
. |
 |
Um fenómeno similar a este aqui apresentado pode ser observado no crescimento dos cornos dos animais.
