UM SISTEMA "ÓPTIMO"
Vejamos um sistema de controlo "óptimo", baseado nas ideias de Verhoeff e na Teoria dos Grupos.
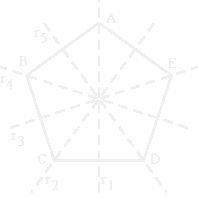
Consideremos um pentágono regular. É fácil verificar que o conjunto das simetrias de um pentágono regular (ao qual é dada a designação de grupo diedral D5) tem apenas 10 elementos (5 rotações e 5 reflexões).

Vamos numerar cada uma dessas simetrias do seguinte modo:
|
0 |
Identidade (Rotação de ângulo 0) |
|
1 |
Rotação de ângulo |
|
2 |
Rotação de ângulo
|
|
3 |
Rotação de ângulo |
|
4 |
Rotação de ângulo
|
|
5 |
Reflexão em relação à recta |
|
6 |
Reflexão em relação à recta |
|
7 |
Reflexão em relação à recta |
|
8 |
Reflexão em relação à recta |
|
9 |
Reflexão em relação à recta |
Vamos também definir uma operação neste conjunto de simetrias. Suponhamos que queremos operar 4 com 8. Para isso, apliquemos ao nosso pentágono [ABCDE] a simetria associada a 4; obtemos o pentágono [BCDEA]:
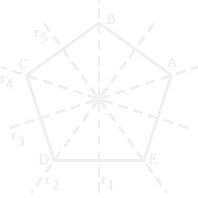
Apliquemos agora a este pentágono a simetria associada ao número 8; obtemos o pentágono [DCBAE]:
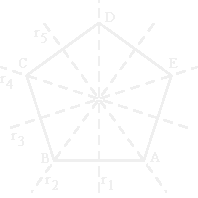
Mas existe
uma simetria na nossa tabela que permite "ir directamente" do pentágono
[ABCDE] para o pentágono [DCBAE], que é a simetria associada a 7.
Logo, consideramos que 4 operado com 8, dá 7. Simbolicamente, denotando
o nosso operador por *, escrevemos que 4 * 8 = 7.
Por um processo análogo a este, podemos concluir que o nosso novo operador
pode ser definido pela tabela:
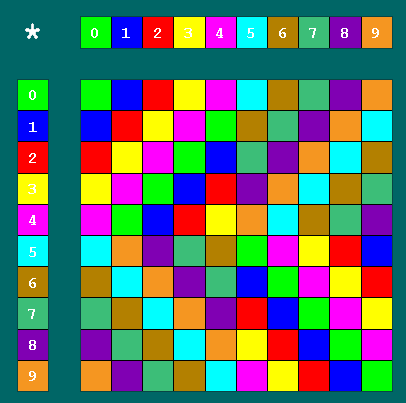
Operação do grupo diedral D5
Note-se que este operador é bastante diferente dos operadores usuais como a soma e a multiplicação aritmética. Em particular, note-se que este operador não é comutativo.
Vejamos um exemplo de um sistema de controlo para números de identificação
com 8 algarismos
x1 x2 x3 x4 x5 x6 x7 x8
usando este operador (de facto, um sistema similar a este serviria para números formados por um qualquer número de algarismos).
Seja C, o nosso algarismo de controlo:
![]()
onde se considera a permutação anti-simétrica
![]() .
.
Para quem não está familiarizado com a notação das permutações, pode encarar esta permutação como sendo uma função tal que:
![]() ,
,
![]() ,
,
![]() ,
, ![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
, ![]() e
e ![]() .
.
Vejamos, por exemplo, o caso do número 12345678. O seu algarismo de controlo será:
![]()
![]()
Agora, seguindo a tabela do operador do grupo diedral D5 , tem-se que 4 * 2 = 1 e, portanto, o algarismo de controlo será
![]()
Procedendo de forma análoga, obtém-se
![]() .
.
Tente calcular o algarismo de controlo de outros números usando este sistema, e confirme os seus resultados no seguinte applet.