Este problema foi denominado problema de Steiner, pela primeira vez, em 1941, no popular livro What is mathematics?, de R. Courant e H. Robbins.
No entanto, já muito antes de Steiner, outros matemáticos como Fermat (1601 - 1665), Torricelli, Cavalieri e Simpson se tinham debruçado sobre as primeiras variantes deste problema.
Tudo começou com um simples problema proposto por Fermat:
|
"Encontrar um ponto no plano cuja soma das distâncias a três pontos dados A, B e C seja mínima." |
Torricelli encontrou uma solução para este problema nos casos em que os ângulos internos do triângulo formado pelos três pontos dados A, B e C são todos menores ou iguais a 120º.
|
|
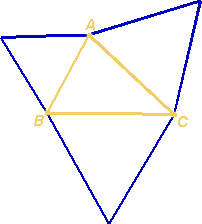
Nos três lados do triângulo [ABC] construir três triângulos equiláteros do lado de fora de [ABC]. |
|
|
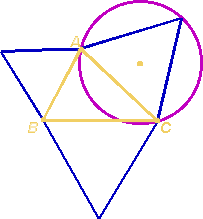
Desenhar as circunferências que circunscrevem cada um destes três triângulos. |
|
|
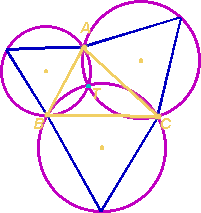
O ponto de intersecção destas três circunferências é o denominado ponto de Torricelli e resolve o problema de Fermat. |
Nos casos em que um dos ângulos internos do triângulo [ABC], por exemplo, o ângulo correspondente ao vértice A, é maior ou igual a 120º, a solução do problema de Fermat é única e coincide com o ponto A. (Note-se que nestes casos o ponto de Torricelli está no exterior do triângulo [ABC] e portanto não pode ser solução para o problema de Fermat.)
Cavalieri encontrou uma propriedade importante do ponto de Torricelli, publicada no seu livro Exercitationes Geometricae de 1647:
|
Quando
o ponto de Torricelli está dentro do triângulo, os ângulos
entre os segmentos que ligam o ponto de Torricelli aos vértices
A, B e C são todos iguais a 120º.
|
Mais tarde, Simpson encontrou outro modo de construir o ponto de Torricelli e publicou-o no seu livro Doctrine and Application of Fluctions de 1750.
|
|
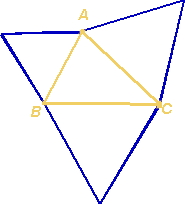
Nos três lados do triângulo [ABC] construir três triângulos equiláteros do lado de fora de [ABC]. |
|
|
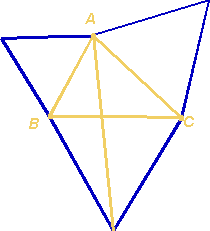
Desenhar os três segmentos de recta que unem cada vértice do triângulo [ABC] ao vértice oposto do triângulo equilátero construído no lado oposto. Estes segmentos de recta são chamados segmentos de Simpson. |
|
|
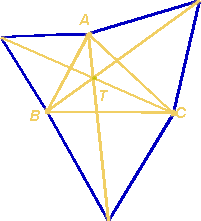
Os três segmentos de Simpson intersectam-se num ponto que coincide com o ponto de Torricelli e que resolve o problema de Fermat. |
Também este método só resolve o problema de Fermat quando os três ângulos internos do triângulo [ABC] são menores ou iguais a 120º.
Mais uma propriedade importante, referida por Heinen em 1834, é a seguinte:
|
Os comprimentos dos segmentos de Simpson são todos iguais à soma das distâncias do ponto de Torricelli aos vértices A, B e C. |
Steiner foi atraído para este problema ao tentar resolver um exercício de generalização do problema de Fermat, proposto por Simpson no seu livro Fluxions:
|
"Encontrar um ponto no plano (ou no espaço Euclidiano d-dimensional) cuja soma das distâncias a n pontos dados A1, ... , An seja mínima." |
Uma outra variante deste problema é a proposta por Jarnik e Kössler em 1934:
|
"Encontrar a mais curta rede que liga n pontos do plano." |
Pode encontrar nas páginas abaixo alguns sketches relativos a este problema.
