|
|
|
|
 |
|
|
|
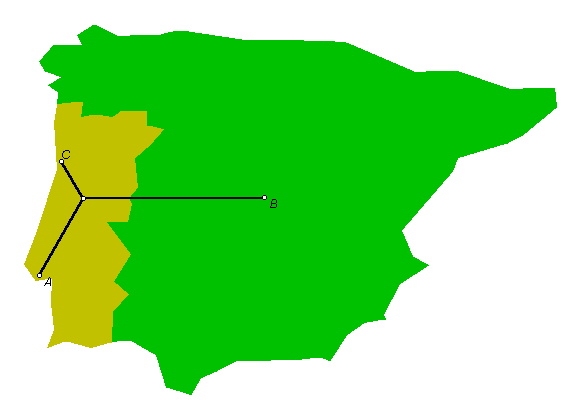
O problema de Steiner consiste em encontrar as redes de comprimento mínimo que ligam um número finito de pontos fixados.
Uma das aplicações
deste problema é a construção de uma rede de estradas
entre determinadas cidades; se o custo for proporcional ao comprimento da
estrada e se não houver mais restrições, a rede de estradas
mais barata é a rede minimal.
|
|
|

|
 |
|
|
|
Outras situações
em que interessa considerar as redes minimais são:
 |
|
 |
|
 |
|
 |
|
Esta página foi realizada no âmbito do estágio do 5º ano do curso de matemática da Faculdade de Ciências da Universidade do Porto por Isabel Cristina Lopes.