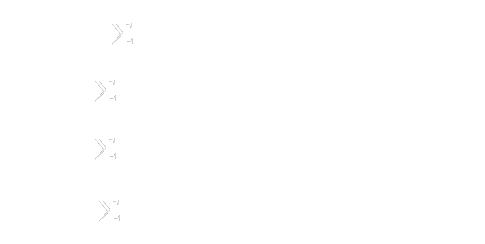Se, dado um polígono inicial de n = 2m lados cujas abcissas dos vértices são x_r, com , tomarmos as diagonais que unem os vértices opostos e unirmos os pontos que dividem essas diagonais em dois segmentos cujo comprimento é, respectivamente, p e 1 - p vezes maior do que o comprimento dessa diagonal, com 0 < p < 1, obtemos um novo polígono de n lados cujas abcissas dos vértices são dadas por

onde x_n+r = x_r, para qualquer . Consideremos a representação de Fourier das abcissas x_r, dada por

Escrevendo o vector (P_j,Q_j) na forma polar , temos

Então, vem

onde d_j = 1 se j é par e d_j = 1 - 2p se j é ímpar. Mais geralmente, vem

Quando k tende para infinito, as parcelas de índice ímpar tendem para zero, pelo que podemos desprezá-las e fazer a seguinte aproximação:

para um valor de k elevado. Note-se que o somatório acima não depende de k, isto é, os pontos da sucessão de polígonos aproximam-se cada vez mais de certos pontos fixos. Estes pontos são os vértices de um polígono de m lados cujas abcissas são dadas por

onde e . Note-se que

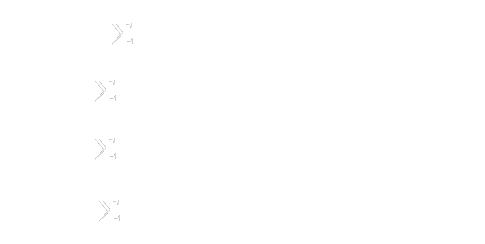
Logo, os vértices deste polígono de m lados são exactamente os pontos médios das diagonais consideradas neste método.

Note-se que a convergência para este polígono é tanto mais rápida quanto o valor 1 - 2p estiver próximo de 0, ou seja, quanto o parâmetro p estiver próximo de 1/2 (se p = 1/2, então este polígono é atingido logo na primeira iteração).