
Quadrado

Seja  um quadrado,
um quadrado,  a medida da sua diagonal e
a medida da sua diagonal e 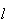 a medida do seu lado. Suponhamos que as duas grandezas são comensuráveis,
isto é,
a medida do seu lado. Suponhamos que as duas grandezas são comensuráveis,
isto é, 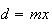 e
e 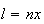 para alguma medida comum
para alguma medida comum 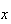 e para alguns números inteiros positivos
e para alguns números inteiros positivos 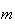 e
e 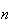 .
.
Marcamos
o ponto 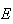 na diagonal
na diagonal ![$\left[ AC\right] $](graphics/quadrado__10.gif) tal que
tal que 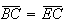 e o ponto
e o ponto 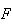 no lado
no lado ![$\left[ AB\right] $](graphics/quadrado__13.gif) tal que
tal que 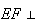
 .
Como
.
Como  ,
o triângulo
,
o triângulo ![$\left[ ABC\right] $](graphics/quadrado__17.gif) é isósceles e, como
é isósceles e, como  ,
temos
,
temos  .
Como
.
Como  e
e 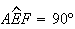 ,
vem
,
vem 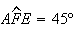 ,
pelo que
,
pelo que ![$\left[ AFE\right] $](graphics/quadrado__23.gif) é isósceles, com
é isósceles, com 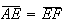 .
Como
.
Como ![$\left[ FBC\right] $](graphics/quadrado__25.gif) e
e ![$\left[ FEC\right] $](graphics/quadrado__26.gif) são triângulos rectângulos com a mesma hipotenusa e com um dos
catetos igual (
são triângulos rectângulos com a mesma hipotenusa e com um dos
catetos igual ( ),
pelo teorema de Pitágoras o outro cateto também é igual,
),
pelo teorema de Pitágoras o outro cateto também é igual, 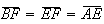 .
.
Construindo
o ponto 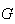 ,
ponto de intersecção da recta paralela a
,
ponto de intersecção da recta paralela a 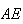 e que passa no ponto
e que passa no ponto 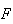 com a recta paralela a
com a recta paralela a 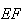 e que passa no ponto
e que passa no ponto 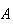 ,
obtemos um novo quadrado
,
obtemos um novo quadrado 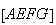 .
Designando por
.
Designando por 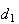 a medida da sua diagonal e
a medida da sua diagonal e 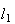 a medida do seu lado, temos:
a medida do seu lado, temos:
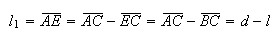
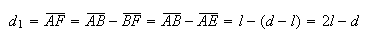
Como  e
e 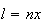 ,
temos:
,
temos:

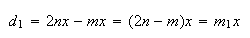
onde  e
e 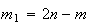 são dois números inteiros positivos, com
são dois números inteiros positivos, com 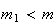 .
De facto,
.
De facto, 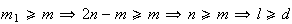 ,
o que é absurdo uma vez que a diagonal de qualquer quadrado é sempre
maior do que o seu lado.
,
o que é absurdo uma vez que a diagonal de qualquer quadrado é sempre
maior do que o seu lado.
Procedendo
da mesma forma com o quadrado 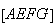 ,
vamos obter um novo quadrado cuja diagonal é
,
vamos obter um novo quadrado cuja diagonal é 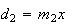 e cujo lado é
e cujo lado é 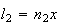 ,
sendo que
,
sendo que 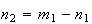 e
e  são dois números inteiros positivos, com
são dois números inteiros positivos, com  .
.
Uma vez que podemos continuar indefinidamente a construir novos quadrados, vamos obter uma sucessão estritamente decrescente de números inteiros positivos:
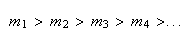
tal que
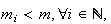 o que é absurdo, dado que não pode haver uma infinidade de números
inteiros positivos distintos menores do que
o que é absurdo, dado que não pode haver uma infinidade de números
inteiros positivos distintos menores do que  (de facto, existem exactamente
(de facto, existem exactamente 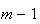 elementos:
elementos: 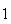 ,
, ,
,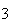 ,...,
,...,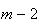 ,
e
,
e 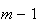 ).
Logo, a diagonal e o lado de
).
Logo, a diagonal e o lado de 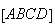 são grandezas incomensuráveis.
são grandezas incomensuráveis.