Dodecágono regular

Consideremos
um dodecágono regular para o qual os pontos 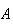 ,
,
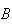 ,
,
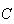 e
e 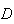 são vértices consecutivos,
são vértices consecutivos, 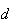 a medida da sua segunda diagonal mais curta e
a medida da sua segunda diagonal mais curta e 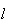 a medida do seu lado. Supondo que
a medida do seu lado. Supondo que 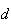 e
e 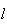 são comensuráveis, temos
são comensuráveis, temos 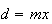 e
e 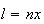 ,
onde
,
onde 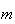 e
e 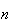 são inteiros positivos e
são inteiros positivos e 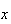 é uma medida comum à segunda diagonal mais curta e ao lado do dodecágono.
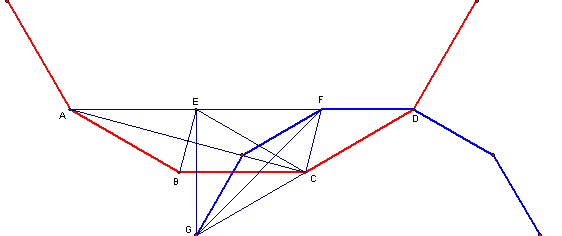
Note-se que cada lado é uma corda da circunferência de centro
é uma medida comum à segunda diagonal mais curta e ao lado do dodecágono.
Note-se que cada lado é uma corda da circunferência de centro 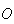 que circunscreve o polígono à qual corresponde um arco de amplitude
que circunscreve o polígono à qual corresponde um arco de amplitude
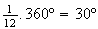 .
Marcamos o ponto
.
Marcamos o ponto 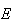 na diagonal
na diagonal ![$\left[ AD\right] $](graphics/dodecagono__17.gif) tal que
tal que 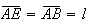 .
Então, como
.
Então, como ![$\left[ AEB\right] $](graphics/dodecagono__19.gif) é isósceles e
é isósceles e 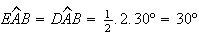 ,
vem
,
vem 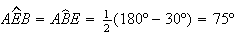 .
Além disso,
.
Além disso, 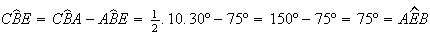 ,
logo a diagonal
,
logo a diagonal ![$\left[ AD\right] $](graphics/dodecagono__23.gif) é paralela ao lado
é paralela ao lado ![$\left[ BC\right] $](graphics/dodecagono__24.gif) .
Marcamos agora o ponto
.
Marcamos agora o ponto 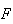 na diagonal
na diagonal ![$\left[ AD\right] $](graphics/dodecagono__26.gif) tal que
tal que 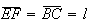 .
Então, como
.
Então, como ![$\left[ EF\right] $](graphics/dodecagono__28.gif) é paralelo a
é paralelo a ![$\left[ BC\right] $](graphics/dodecagono__29.gif) ,
,
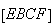 é um paralelogramo, pelo que
é um paralelogramo, pelo que 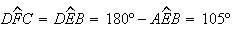 .
Como
.
Como 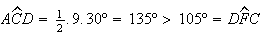 ,
queremos ter um ponto
,
queremos ter um ponto 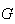 na semi-recta
na semi-recta 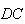 tal que
tal que 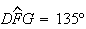 .
Seja
.
Seja 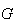 o ponto na semi-recta
o ponto na semi-recta 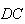 tal que
tal que 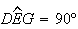 .
Como
.
Como ![$\left[ AE\right] $](graphics/dodecagono__39.gif) é paralelo a
é paralelo a ![$\left[ BC\right] $](graphics/dodecagono__40.gif) e
e 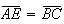 ,
,
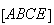 é um paralelogramo, pelo que
é um paralelogramo, pelo que 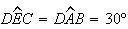 .
Então, vem
.
Então, vem 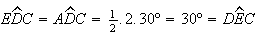 e
e ![$\left[ ECD\right] $](graphics/dodecagono__45.gif) é um triângulo isósceles, com
é um triângulo isósceles, com 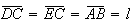 .
Como
.
Como 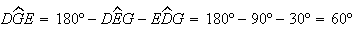 e
e 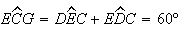 ,
o triângulo
,
o triângulo ![$\left[ EGC\right] $](graphics/dodecagono__49.gif) é equilátero, com
é equilátero, com 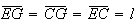 .
Além disso, como
.
Além disso, como 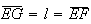 ,
o triângulo rectângulo
,
o triângulo rectângulo ![$\left[ FEG\right] $](graphics/dodecagono__52.gif) é isósceles, pelo que
é isósceles, pelo que 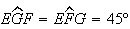 .
Logo,
.
Logo, 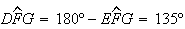 ,
como pretendíamos.
,
como pretendíamos.
Como 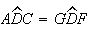 e
e 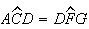 ,
temos que os triângulos
,
temos que os triângulos ![$\left[ ACD\right] $](graphics/dodecagono__57.gif) e
e ![$\left[ DFG\right] $](graphics/dodecagono__58.gif) são semelhantes, pelo que
são semelhantes, pelo que ![$\left[ DG\right] $](graphics/dodecagono__59.gif) é a segunda diagonal mais curta de um dodecágono regular de lado
é a segunda diagonal mais curta de um dodecágono regular de lado ![$\left[ DF\right] $](graphics/dodecagono__60.gif) .
Sendo assim, podemos construir um dodecágono regular que passa pelos pontos
.
Sendo assim, podemos construir um dodecágono regular que passa pelos pontos
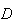 ,
,
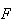 e
e 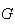 ,
cujas medidas do lado e da segunda diagonal mais curta são dadas por:
,
cujas medidas do lado e da segunda diagonal mais curta são dadas por:
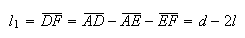
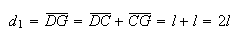
Como 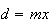 e
e 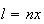 ,
temos:
,
temos:
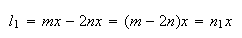
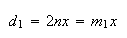
onde 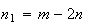 e
e 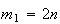 são dois números inteiros positivos, com
são dois números inteiros positivos, com 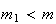 .
De facto,
.
De facto, 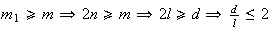 ,
o que é absurdo uma vez que
,
o que é absurdo uma vez que 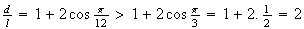 .
Procedendo da mesma forma, vamos obter um novo dodecágono regular cuja
segunda diagonal mais curta é
.
Procedendo da mesma forma, vamos obter um novo dodecágono regular cuja
segunda diagonal mais curta é 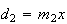 e cujo lado é
e cujo lado é 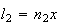 ,
sendo que
,
sendo que 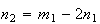 e
e 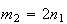 são dois números inteiros positivos, com
são dois números inteiros positivos, com 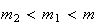 .
.
Uma vez que podemos continuar indefinidamente a construir novos dodecágonos regulares, vamos obter uma sucessão estritamente decrescente de números inteiros positivos:
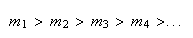
tal que
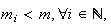 o que é absurdo, dado que não pode haver uma infinidade de números
inteiros positivos distintos menores do que
o que é absurdo, dado que não pode haver uma infinidade de números
inteiros positivos distintos menores do que 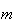 (de facto, existem exactamente
(de facto, existem exactamente 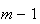 elementos:
elementos: 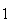 ,
,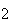 ,
,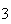 ,...,
,...,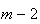 ,
e
,
e 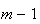 ).
Logo, a segunda diagonal mais curta e o lado do dodecágono regular são
grandezas incomensuráveis.
).
Logo, a segunda diagonal mais curta e o lado do dodecágono regular são
grandezas incomensuráveis.