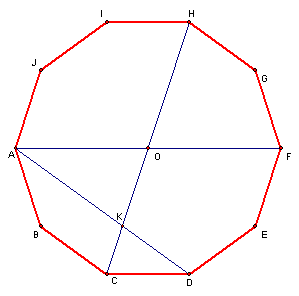
Decágono regular

Seja  um decágono regular de centro em
um decágono regular de centro em 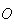 cujas medidas do lado, da diagonal mais longa e da segunda diagonal mais curta
são
cujas medidas do lado, da diagonal mais longa e da segunda diagonal mais curta
são 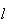 ,
,
 e
e 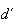 ,
respectivamente. Sejam
,
respectivamente. Sejam ![$\left[ AF\right] $](graphics/decagono3__6.gif) e
e ![$\left[ CH\right] $](graphics/decagono3__7.gif) duas diagonais que passam pelo centro do decágono,
duas diagonais que passam pelo centro do decágono, ![$\left[ AD\right] $](graphics/decagono3__8.gif) a segunda diagonal mais curta que une os vértices
a segunda diagonal mais curta que une os vértices  e
e 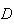 ,
e
,
e 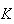 o ponto de intersecção da diagonal
o ponto de intersecção da diagonal ![$\left[ AD\right] $](graphics/decagono3__12.gif) com a diagonal
com a diagonal ![$\left[ CH\right] $](graphics/decagono3__13.gif) .
Então,
.
Então, 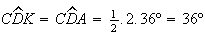 e
e  ,
pelo que
,
pelo que  e
e ![$\left[ KCD\right] $](graphics/decagono3__17.gif) é um triângulo isósceles, com
é um triângulo isósceles, com  .
Além disso,
.
Além disso, 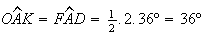 ,
,
 e
e  ,
pelo que
,
pelo que ![$\left[ AOK\right] $](graphics/decagono3__22.gif) é um triângulo isósceles, com
é um triângulo isósceles, com 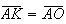 .
Portanto, a medida da diagonal mais longa é dada por:
.
Portanto, a medida da diagonal mais longa é dada por:

Logo, vem:

Equivalentemente, temos:

Assim,
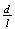 será um número racional se e só se
será um número racional se e só se 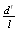 também o fôr, o que já vimos que não acontece. Portanto,
a diagonal mais longa e o lado do decágono
também o fôr, o que já vimos que não acontece. Portanto,
a diagonal mais longa e o lado do decágono  são grandezas incomensuráveis.
são grandezas incomensuráveis.