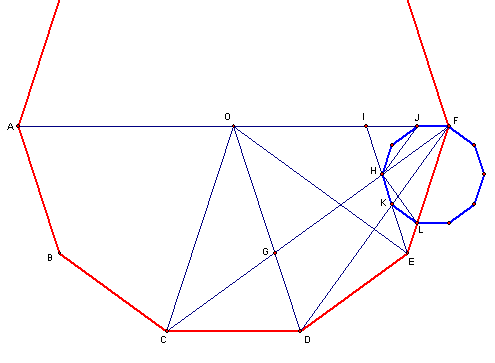
Decágono regular

Consideremos
um decágono regular para o qual os pontos 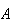 ,
,
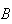 ,
,
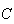 ,
,
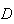 ,
,
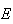 e
e 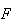 são vértices consecutivos,
são vértices consecutivos, 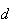 a medida da sua diagonal mais longa e
a medida da sua diagonal mais longa e 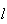 a medida do seu lado. Supondo que
a medida do seu lado. Supondo que 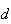 e
e 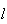 são comensuráveis, temos
são comensuráveis, temos 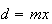 e
e 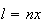 ,
onde
,
onde 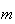 e
e 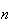 são inteiros positivos e
são inteiros positivos e 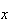 é uma medida comum à segunda diagonal mais curta e ao lado do decágono.
Note-se que cada lado é uma corda da circunferência que circunscreve
o polígono à qual corresponde um arco de amplitude
é uma medida comum à segunda diagonal mais curta e ao lado do decágono.
Note-se que cada lado é uma corda da circunferência que circunscreve
o polígono à qual corresponde um arco de amplitude 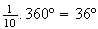 .
Marcamos os pontos
.
Marcamos os pontos 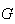 e
e  na diagonal
na diagonal ![$\left[ CF\right] $](graphics/decagono2__19.gif) tal que
tal que 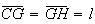 .
Então, como
.
Então, como ![$\left[ CDG\right] $](graphics/decagono2__21.gif) é isósceles e
é isósceles e 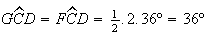 ,
vem
,
vem 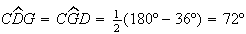 .
Além disso,
.
Além disso, 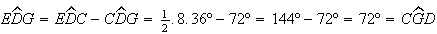 ,
logo a diagonal
,
logo a diagonal ![$\left[ CF\right] $](graphics/decagono2__25.gif) é paralela ao lado
é paralela ao lado ![$\left[ DE\right] $](graphics/decagono2__26.gif) .
Então, como
.
Então, como ![$\left[ GH\right] $](graphics/decagono2__27.gif) é paralelo a
é paralelo a ![$\left[ DE\right] $](graphics/decagono2__28.gif) e
e 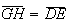 ,
temos que
,
temos que 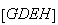 é um paralelogramo, sendo
é um paralelogramo, sendo 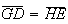 e
e 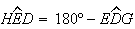 .
Como
.
Como 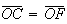 ,
,
![$\left[ OCF\right] $](graphics/decagono2__34.gif) é um triângulo isósceles, com
é um triângulo isósceles, com 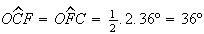 .
Temos então que
.
Temos então que  ,
pelo que
,
pelo que ![$\left[ OCG\right] $](graphics/decagono2__37.gif) é um triângulo isósceles, com
é um triângulo isósceles, com 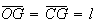 .
Logo,
.
Logo, 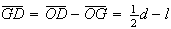 .
.
Seja 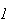 o ponto de intersecção da recta
o ponto de intersecção da recta 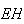 com a diagonal
com a diagonal ![$\left[ AF\right] $](graphics/decagono2__42.gif) .
Como
.
Como 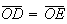 ,
,
![$\left[ ODE\right] $](graphics/decagono2__44.gif) é um triângulo isósceles, com
é um triângulo isósceles, com 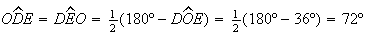 .
Logo,
.
Logo, 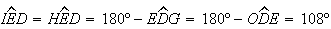 ,
,
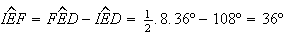 ,
,
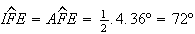 e
e 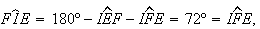 pelo que
pelo que ![$\left[ IEF\right] $](graphics/decagono2__50.gif) é um triângulo isósceles, com
é um triângulo isósceles, com  .
Então, vem
.
Então, vem 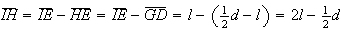 .
Temos também que
.
Temos também que 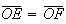 ,
logo
,
logo ![$\left[ OEF\right] $](graphics/decagono2__54.gif) é um triângulo isósceles, com
é um triângulo isósceles, com 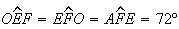 ,
pelo que
,
pelo que  e
e ![$\left[ IOE\right] $](graphics/decagono2__57.gif) é um triângulo isósceles, com
é um triângulo isósceles, com 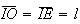 .
.
Seja 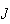 o ponto do segmento
o ponto do segmento ![$\left[ IF\right] $](graphics/decagono2__60.gif) tal que
tal que 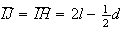 (note-se que
(note-se que 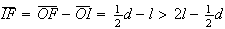 ,
dado que
,
dado que 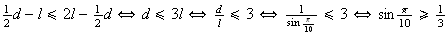 ,
e isto é absurdo uma vez que
,
e isto é absurdo uma vez que 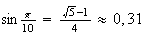 ).
Então,
).
Então, ![$\left[ IHJ\right] $](graphics/decagono2__65.gif) é um triângulo isósceles, com
é um triângulo isósceles, com 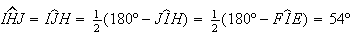 .
Mas então
.
Mas então 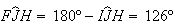 e
e 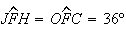 ,
pelo que
,
pelo que ![$\left[ JFH\right] $](graphics/decagono2__69.gif) é semelhante ao triângulo
é semelhante ao triângulo ![$\left[ DCF\right] $](graphics/decagono2__70.gif) ,
uma vez que
,
uma vez que 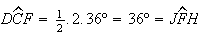 e
e 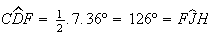 .
.
Assim,
podemos construir um decágono regular que passa pelos pontos 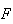 ,
,
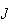 e
e 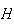 ,
sendo
,
sendo ![$\left[ FJ\right] $](graphics/decagono2__76.gif) um dos seus lados e
um dos seus lados e ![$\left[ JH\right] $](graphics/decagono2__77.gif) uma das suas segundas diagonais mais curtas. Note-se que um dos vértices
deste novo decágono encontra-se na diagonal
uma das suas segundas diagonais mais curtas. Note-se que um dos vértices
deste novo decágono encontra-se na diagonal ![$\left[ DF\right] $](graphics/decagono2__78.gif) (mais propriamente, é o ponto de intersecção de
(mais propriamente, é o ponto de intersecção de ![$\left[ DF\right] $](graphics/decagono2__79.gif) com
com ![$\left[ IE\right] $](graphics/decagono2__80.gif) ,
uma vez que
,
uma vez que 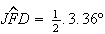 e
e 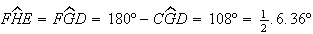 )
e outro vértice encontra-se no lado
)
e outro vértice encontra-se no lado ![$\left[ EF\right] $](graphics/decagono2__83.gif) (uma vez que
(uma vez que 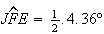 ).
Sejam
).
Sejam 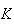 e
e 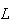 estes dois pontos, respectivamente. Temos que
estes dois pontos, respectivamente. Temos que 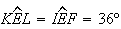 e
e 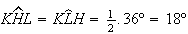 ,
logo
,
logo 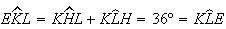 e
e ![$\left[ KEL\right] $](graphics/decagono2__90.gif) é um triângulo isósceles, com
é um triângulo isósceles, com 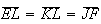 .
Logo, as medidas do lado e da diagonal mais longa são dadas por:
.
Logo, as medidas do lado e da diagonal mais longa são dadas por:
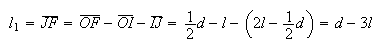
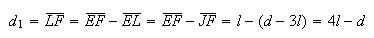
Como 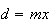 e
e 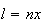 ,
temos:
,
temos:
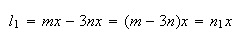

onde 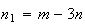 e
e 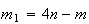 são dois números inteiros positivos, com
são dois números inteiros positivos, com 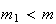 .
De facto,
.
De facto, 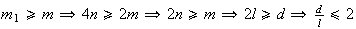 ,
o que é absurdo uma vez que
,
o que é absurdo uma vez que 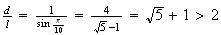 .
.
Procedendo
da mesma forma, vamos obter um novo decágono regular cuja segunda diagonal
mais curta é 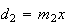 e cujo lado é
e cujo lado é 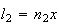 ,
sendo que
,
sendo que 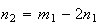 e
e 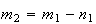 são dois números inteiros positivos, com
são dois números inteiros positivos, com  .
.
Uma vez que podemos continuar indefinidamente a construir novos decágonos regulares, vamos obter uma sucessão estritamente decrescente de números inteiros positivos:
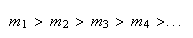
tal que
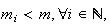 o que é absurdo, dado que não pode haver uma infinidade de números
inteiros positivos distintos menores do que
o que é absurdo, dado que não pode haver uma infinidade de números
inteiros positivos distintos menores do que 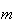 (de facto, existem exactamente
(de facto, existem exactamente 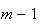 elementos:
elementos: 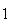 ,
,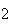 ,
,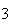 ,...,
,..., ,
e
,
e 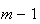 ).
Logo, a diagonal mais longa e o lado do decágono regular são grandezas
incomensuráveis.
).
Logo, a diagonal mais longa e o lado do decágono regular são grandezas
incomensuráveis.