TORO – conhecer a superfície

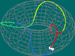
Podemos pensar um toro (leia-se, superfície do toro) como sendo a superfície que se obtém colando (sem torcer) os pares de lados paralelos de um rectângulo. Colando apenas um par obtemos um cilindro (uma secção de um cilindro generalizado), e colando os "topos" desse cilindro obtemos um toro.

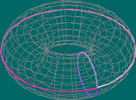
Há, então, uma identificação dos pontos do rectângulo com os pontos do toro.

(u,v)(Cos[u] (r2 + r1 Cos[v]), Sin[u] (r2 + r1 Cos[v]), r1 Sin[v])

Os pares de lados paralelos do rectângulo correspondem à mesma linha no toro. Há, portanto, uma identificação dos pontos dos lados paralelos, ilustrada pela sua coloração.

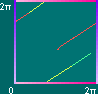Desenhar uma curva no toro que atravesse uma das linhas de colagem, corresponde, no rectângulo, a "sair" por um lado e "entrar" pelo outro lado a partir do ponto correspondente.

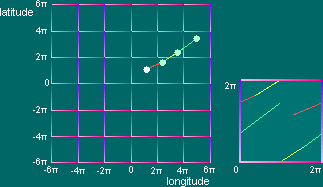
A longitude e a latitude dos pontos dão-nos coordenadas da sua localização sobre a superfície. Ambas são medidas de ângulos (em radianos) em redor da superfície. A latitude é medida sobre um meridiano e diz-nos em que paralelo está o ponto, dando-nos como que a altura do ponto (dá-nos um pouco mais que isso...). A longitude é medida sobre um paralelo e diz-nos em que meridiano está o ponto. Para a identificação da localização de um ponto sobre o cilindro precisamos apenas que a longittude e a latitude variem em intervalos de [0,2[, pois cobrem toda a superfície.


No entanto, para que possamos também identificar o ponto na curva de forma contínua, podemos estender esses intervalos a intervalos múltiplos I e J sob a seguinte identificação:

I x J
[0,2[ x [0,2[
(u,v)
(Mod[u, 2],Mod[v, 2])

Esta extensão materializa-se nos applets com uma mudança de escala, permitindo, assim, de forma mais cómoda analisar curvas que dão várias voltas.

E este levantamento dos caminhos no toro pode ainda ser alargado a todo o plano, permitindo, ao mesmo tempo, o estudo de todas as curvas sobre o toro, sem restrição do número de voltas. Consideraríamos, de forma análoga, uma infinidade de "cópias" do rectângulo inicial, devidamente alinhadas (nas duas direcções), podendo então dizer-se que cada ponto do plano se projecta num ponto do toro e que cada ponto do toro admite uma infinidade de levantamentos no plano, um em cada um dos rectângulos.