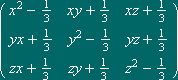Representação
em  3
do espaço projectivo de dimensão 2 |
Consideremos,
no espaço vectorial M
de dimensão 9
constituído pelas matrizes 3x3,
o produto interno usual (identificação com 
9).
Notemos Msim o subespaço vectorial de dimensão 6 de M constituído pelas matrizes simétricas e Msim1 o subespaço afim de dimensão 5 deste último formado pelas matrizes simétricas de traço 1.
O espaço
projectivo 
2(
) é difeomorfo
a um subconjunto P2(
)
de Msim1
pelo difeomorfismo 
que a cada subespaço vectorial de dimensão 1
de 3 associa
a matriz da projecção ortogonal de 3
sobre esse subespaço. Se (x,y,z)
3
tem norma 1, a
matriz que corresponde ao subespaço vectorial gerado por (x,y,z)
é a matriz
 |
. |
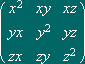De facto,
a imagem P2(
) do
projectivo está contida na intersecção com Msim1
da hipersuperfície esférica S
de centro O
e raio 1 de Msim.
Um dos
elementos de S 
Msim
que não pertence a P2(
) é
a matriz
A= |
 |
. |
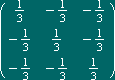A projecção
estereográfica 
,
a partir de A,
é um difeomorfismo de S
\ {A} sobre o subespaço vectorial F
de dimensão 5 de
Msim
constituído pelas matrizes simétricas ortogonais a
A e está definida explicitamente por
| (X)
= |
 |
. |
Ela aplica
P2(
) no
subespaço afim F
Msim1
de dimensão 4 de
Msim,
constituído pelas matrizes
Y= |
 |
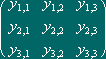que verificam as condições y1,1 + y2,2 + y3,3 = 1 e y1,2 + y1,3 + y2,3 = 1/2.
Chegados
a este ponto iniciamos uma fase da tentativa: Para tentar meter o projectivo
em 3
(naturalmente com auto-intersecções mas, se possível,
sem muita maldade) experimentamos compor o difeomorfismo
º com uma aplicação
afim de F
Msim1
para 3
que se revele razoável. A segunda tentativa corresponde a considerar
a aplicação afim que à matriz Y
associa (y1,1,
y1,2 + y2,3,
y3,3). Depois de compor ainda
com uma translação de 3
(que equivale a ignorar a parcela A
de (X)
), obtemos a aplicação de 2(
) que a cada subespaço
vectorial gerado pelo vector (x,y,z)
de norma 1, com a correspondente
matriz
X= |
|
, |
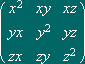associa a imagem, pela aplicação afim, da referida matriz
 |
|
|||
|
Consideremos enfim o espaço projectivo como imagem do hemisfério
norte da superfície esférica unitária de centro na origem
de 3,
parametrizada pela latitude u
[0,
/2]
e pela longitude v
[0,2],
através de
| x = cos(u) cos(v) |
| y = cos(u) sin(v) |
| z = sin(u), |
o que
conduz à parametrização da imagem do espaço projectivo,
que a (u,v)
associa o elemento de 3
com as três coordenadas
 |
 |
 |
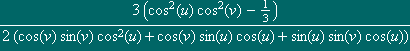
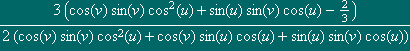
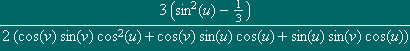