No plano
Euclidiano, podemos definir ângulo como sendo uma região determinada por duas
semi-rectas com a mesma origem. As semi-rectas são os lados do ângulo e a origem
das semi-rectas é o vértice do ângulo.
Analogamente,
na esfera, um ângulo é uma região delimitada por dois semi-círculos máximos
que se intersectam em dois pontos antípodas. Qualquer um dos pontos antípodas
é designado o vértice do ângulo e os semi-círculos
máximos são os lados do ângulo.
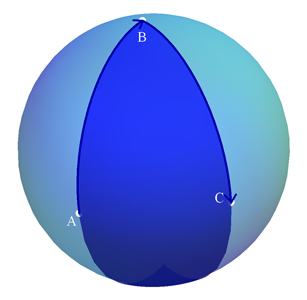
Como dois semi-círculos máximos
definem duas regiões disjuntas, é preciso distinguir a qual delas
nos referimos quando falamos em ângulo. Para não haver ambiguidade
sobre a região a que nos estamos a referir, vamos considerar ângulos
orientados: considerando pontos distintos A, B
e C onde B é o vértice do ângulo
e A e C pertencem a cada um dos lados, chamaremos
ângulo ABC à região que está sempre à direita do caminho
orientado que vai de A para B e de B
para C.
|
|
|

A amplitude do ângulo corresponde
à amplitude do ângulo orientado formado pelos semi-planos que contêm
os lados do ângulo, ou seja, os semi-planos que contêm os semi-círculos.
|
|

