Pense num número natural abc com três dígitos, sendo a≠c. Depois, secretamente, inverta-o, obtendo cba, e calcule a diferença do maior pelo menor. Bastará agora que nos indique o primeiro dígito dessa diferença para lhe revelarmos o resultado.

No artigo "Dinâmica de um truque" do Atractor, na Gazeta de Matemática, este truque é explicado. Nele também se estudam as órbitas da função f que actua no conjunto dos números naturais com três dígitos (permitindo-se zeros à esquerda) e que a cada número associa a distância dele para a sua versão invertida.

Nesta situação, pode verificar-se que 000 é um ponto fixo de f, que atrai todos os números abc com a=c; e

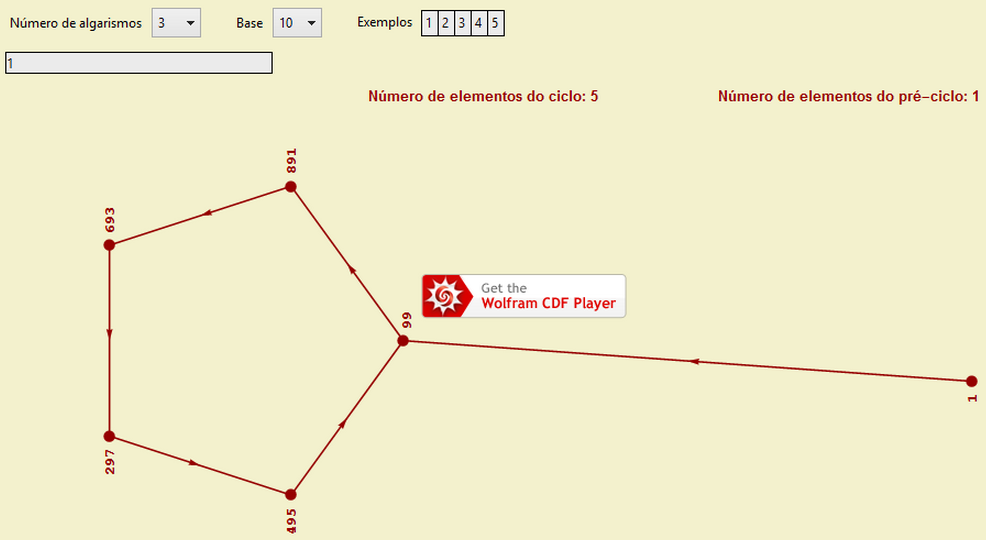
099->891->693->297->495

é um ciclo de período 5 a que chegam todas as outras órbitas em não mais do que duas iterações de f (figura seguinte).

No artigo, é ainda analisado o que se passa se, em vez de números com 3 algarismos, partirmos de números com 1, 2, 4 ou mais algarismos. E se considerarmos outra base que não a base 10?

Consulte algumas conjecturas sobre o problema e não perca a aplicação interactiva que permite descobrir a órbita de uma representação à escolha, com até 10 algarismos, numa qualquer base entre 2 e 10.