resultaram da sua medição directa. Por este método podia-se obter
com uma ou duas casas decimais, o que era certamente suficiente para as
necessidades práticas da Antiguidade.
As primeiras estimativas para
resultaram da sua medição directa. Por este método podia-se obter
com uma ou duas casas decimais, o que era certamente suficiente para as
necessidades práticas da Antiguidade.
No entanto, mesmo nessa altura havia quem se dedicasse ao
cálculo de
para além de qualquer necessidade prática.
O primeiro a conseguir resultados nesse campo foi Arquimedes
que apresentou um método geométrico para o cálculo de
,
hoje conhecido pelo seu nome. O método consiste em circunscrever e inscrever
um polígono de n lados para uma dada circunferência.
O perímetro da circunferência estaria compreendido entre os perímetros dos polígonos.
Deste modo conseguiu deduzir que o valor de
estaria compreendido entre
 |
|
|
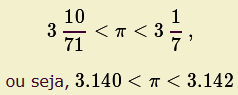Este terá sido o sinal de partida para a corrida iniciada
pelos caçadores de dígitos de
.
A partir deste método foram deduzidas inúmeras fórmulas que
foram permitindo calcular
com cada vez mais precisão.
Outros métodos foram entretanto descobertos e permitiam obter
mais rapidamente, até chegarmos aos algoritmos utilizados actualmente e que
permitem em cada iteração quadruplicar e mais, o número de dígitos calculados.
.
Na tabela que se apresenta a seguir faz-se um resumo das
etapas mais significativas para o cálculo de
ao longo dos tempos.
 |
 |
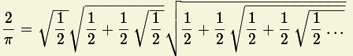De fácil utilização mas de convergência lenta para
.
 |
 |
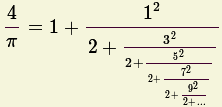Abriu as portas a uma nova era para o cálculo de
uma vez que arctan(1) =
.
Fórmula de convergência muito lenta para
.
Foi publicada por Leibnitz em 1673.
 |
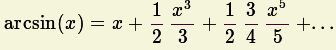arcsin(
) =
. De convergência mais rápida que a fórmula de
Gregory/Leibnitz.
 |
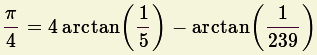Esta fórmula convergente muito mais rapidamente que arctan(1).
Com ela Machin calculou os 100 primeiros
algarismos significativos de
.
Marcou o início de uma nova era.
 |
.
Somente alguns exemplos,
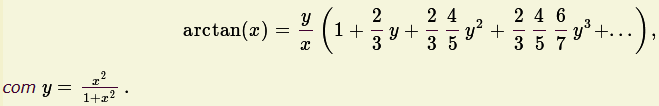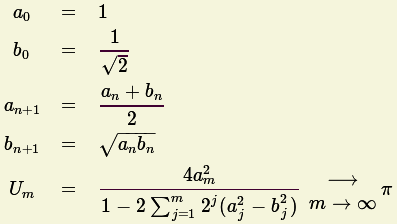
Início da era moderna para o cálculo de
.
Com este algoritmo, em cada iteração, o número de algarismos
significativos calculados correctamente para
duplica.
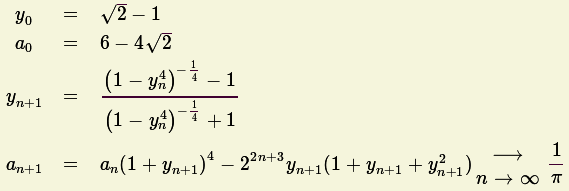
Baseados nos trabalhos de Ramanujan.
Em cada iteração, é quadruplicado o número correcto de dígitos
calculados.
Por isso se diz um algoritmo de 4aordem.
 |
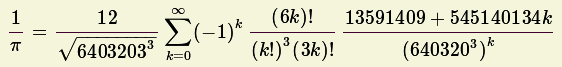Fórmula derivada com auxílio de um manipulador
simbólico matemático.
 |
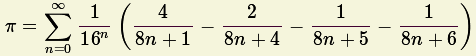Esta fórmula foi publicada em 1997 e permite calcular o
n-ésimo dígito hexadecimal de
.
Na página seguinte apresentam-se alguns resultados
calculados para o valor de
ao longo dos tempos, baseados nalguns dos métodos descritos.
Como
calcular
com um bilião de algarismos significativos
