PARA SABER MAIS...
CHAVES COBERTAS QUE GARANTEM O 2º PRÉMIO
Num jogo de totobola com n partidas, existem \(3^{n}\) chaves possíveis, pois em cada partida pode-se escolher um de três resultados possíveis: 1, X ou 2.
Quando se aposta numa determinada chave, esta garante o 1º prémio caso a chave vencedora seja essa mesma, ou seja, se se acertar nos resultados das n partidas. Contudo, essa chave garante o 2º prémio em mais casos: quando a chave vencedora difere da chave apostada somente no resultado de uma partida, ou seja, quando se acerta no resultado de n-1 partidas. Assim, em relação a garantir pelo menos o 2º prémio, cada aposta simples cobre a respectiva chave, que corresponde ao 1º prémio, e cobre também as chaves que diferem da aposta apenas no resultado de uma partida. Portanto, para além da própria, cada aposta simples cobre 2n chaves, pois, das n partidas, podemos falhar numa delas de duas formas diferentes.
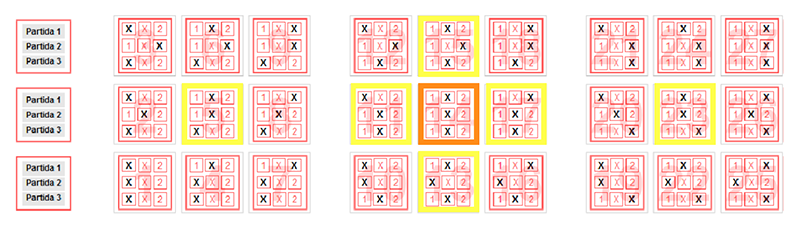
Para um jogo com 3 partidas, a chave X-X-X cobre as seguintes chaves vencedoras: X-X-X (1º prémio); 1-X-X e 2-X-X (2º prémio - falha a 1ª partida); X-1-X e X-2-X (2º prémio - falha a 2ª partida); X-X-1 e X-X-2 (2º prémio - falha a 3ª partida). |
Num jogo de totobola constituído por n partidas, cada aposta simples cobre 2n+1 chaves que garantem, no mínimo, o 2º prémio.