ATRACTOR

Por vezes os diagramas podem ser enganadores!

Consideremos a seguinte soma:

\(1+\frac{1}{4}+\frac{1}{9}+\frac{1}{16}+\frac{1}{25}+...+\frac{1}{n^{2}}+...=?\)

Esta soma pode ser representada pela região cinzenta do gráfico seguinte (onde cada bloco corresponde a uma parcela):

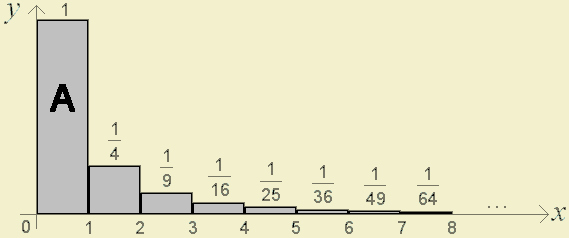
(Observação: As escalas consideradas para o eixo do \(x\) e do \(y\) são diferentes.)

Então, por comparação de cada bloco correspondente, tem-se que a soma anterior é menor que a área colorida no gráfico seguinte:

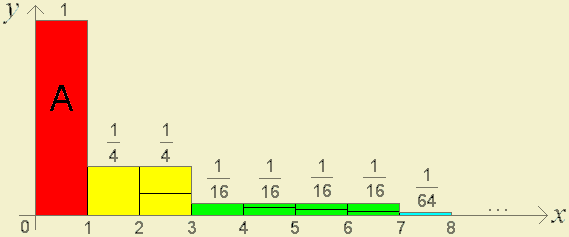
De facto,

\(\begin{array}{ccc} 1+\frac{1}{4}+\frac{1}{9}+\frac{1}{16}+\frac{1}{25}+...+\frac{1}{n^{2}}+...\\ =\\ 1 & = & 1\\ +\frac{1}{4}+\frac{1}{9} & < & 2\times\frac{1}{4}=\frac{1}{2}\\ +\frac{1}{16}+\frac{1}{25}+\frac{1}{36}+\frac{1}{49} & < & 4\times\frac{1}{16}=\frac{1}{4}\\ +\frac{1}{8^{2}}+\frac{1}{9^{2}}+...+\frac{1}{15^{2}} & < & 8\times\frac{1}{64}=\frac{1}{8}\\ ... & ... & ...\\ +\frac{1}{(2^{n})^{2}}+\frac{1}{(2^{n}+1)^{2}}+...+\frac{1}{(2^{n}+(2^{n}-1))^{2}} & < & 2^{n}\times\frac{1}{(2^{n})^{2}}=\frac{1}{2^{n}}\\ ... & ... & ... \end{array}\)

e, portanto,

\(1+\frac{1}{4}+\frac{1}{9}+\frac{1}{16}+\frac{1}{25}+...+\frac{1}{n^{2}}+...<1+\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+...+\frac{1}{2^{n}}+...=2\)

Assim, se precisássemos de uma lata de tinta cinzenta para pintar o quadrilátero A (de área 1) no primeiro gráfico, necessitaríamos de duas latas de tinta (sobrando alguma tinta) para pintar toda a região cinzenta.

Considemos agora a soma

\(1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\frac{1}{5}+\frac{1}{6}+...+\frac{1}{n}+...\)

e o gráfico que a representa.

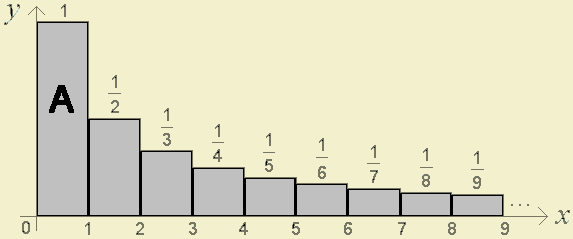
Coloquemos agora o mesmo problema: Quantas latas de tinta seriam necessárias para pintar a região cinzenta? Comparando esta figura com a primeira, somos tentados a dizer que basta um pouco mais de tinta (talvez três ou quatro latas de tinta). Mas será que é assim? Façamos uma análise semelhante à que foi feita na primeira soma considerada. Tem-se

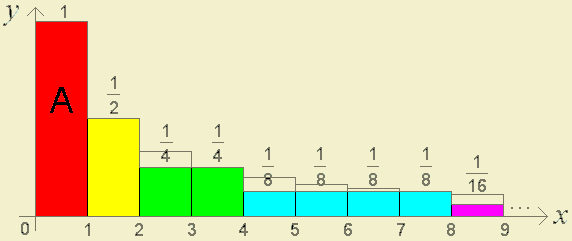
ou seja,

\(\begin{array}{ccc} 1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\frac{1}{5}+...+\frac{1}{n}+...\\ =\\ 1 & = & 1\\ +\frac{1}{2} & = & \frac{1}{2}\\ +\frac{1}{3}+\frac{1}{4} & >& 2\times\frac{1}{4}=\frac{1}{2}\\ +\frac{1}{5}+\frac{1}{6}+\frac{1}{7}+\frac{1}{8} & > & 4\times\frac{1}{8}=\frac{1}{2}\\ +\frac{1}{9}+\frac{1}{10}+...+\frac{1}{16} & > & 8\times\frac{1}{16}=\frac{1}{2}\\ ... & ... & ...\\ +\frac{1}{(2^{n}+1)}+\frac{1}{(2^{n}+2)}+...+\frac{1}{(2^{n+1})} & > & 2^{n}\times\frac{1}{(2^{n+1})}=\frac{1}{2}\\ ... & ... & ... \end{array}\)

e, portanto,

\(1+\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+\frac{1}{5}+\frac{1}{6}+...+\frac{1}{n}+...>1+\frac{1}{2}+\frac{1}{2}+\frac{1}{2}+\frac{1}{2}+...\)

Isto significa que não existe tinta suficiente no universo para pintar toda a região colorida, o que contraria a nossa previsão de que três ou quatro latas de tinta seriam suficientes.

Conclusão:

Apesar de ambos os diagramas serem bastantes parecidos as propriedades das somas que representam são bastante distintas. O erro desta vez não foi de falta de rigor na elaboração dos diagramas, mas sim do facto de estes só representarem uma pequena parte (finita) da soma total (que tem um número infinito de parcelas) e portanto não servirem para tirarmos conclusões imediatas sobre a soma total. Quando passamos do finito para o infinito em Matemática podemos encontrar muitas surpresas!