Cilindro - Conhecer a superfície
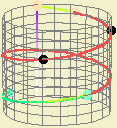
Podemos pensar um cilindro (leia-se, superfície cilíndrica) como sendo a superfície que se obtém colando (sem torcer) um par de lados paralelos de um rectângulo. Os lados não colados formam, assim, curvas fechadas, como se de circunferências se tratassem.
Há, então, uma identificação dos pontos desse rectângulo com os pontos do cilindro. \[(u,v)\rightarrow(r\cos(u),r\sen(u),v).\]Os pontos dos lados do rectângulo que serão colados correspondem ao mesmo segmento no cilindro. Há, portanto, uma identificação dos pontos do par de lados paralelos, ilustrada pela sua coloração.
Desenhar uma curva no cilindro que atravesse a linha de colagem, corresponde, no rectângulo, a "sair" por um lado e "entrar" pelo outro a partir do ponto correspondente (à mesma altura).
A longitude e a latitude dos pontos dão-nos coordenadas da sua localização sobre a superfície. A latitude varia num intervalo \(I\) fechado de \(\mathbb{R}\) e é medida em altura (no caso das apps consideradas). A longitude é a medida de um ângulo (em radianos) em redor da superfície. Para a identificação da localização de um ponto sobre o cilindro precisamos apenas que a longitude varie no intervalo \(\left[0,2\pi\right[\), pois cobre toda a superfície.
No entanto, para que possamos também identificar o ponto na curva de forma contínua, podemos estender esse intervalo a intervalos múltiplos \(J\) sob a seguinte identificação: \[\begin{array}{ccc} J\times I & \rightarrow & \left[0,2\pi\right[\times I\\ (u,v) & \rightarrow & (\mbox{Mod}\left[u,2\pi\right],v) \end{array}\]
Esta extensão materializa-se nas apps com uma mudança de escala, permitindo, assim, de forma mais cómoda analisar curvas que dão várias voltas.
E este levantamento dos caminhos no cilindro pode ainda ser alargado a uma tira infinita do plano, permitindo, ao mesmo tempo, o estudo de todas as curvas sobre o cilindro, sem restrição do número de voltas. Consideraríamos, de forma análoga, uma infinidade de "cópias" do rectângulo inicial, devidamente alinhadas, podendo, então, dizer-se que cada ponto da tira do plano se projecta num ponto do cilindro e que cada ponto do cilindro admite uma infinidade de levantamentos na tira, um em cada um dos rectângulos.