ATRACTOR

Let \(f:\, I\rightarrow\mathbb{R}^{2}\) be a differentiable parametrized curve. For each \(t\in I\) with \(f'(t) \neq 0\), there is a unique line that passes through point \(f(t)\) and has the direction of the vector \(f'(t)\). This is the tangent line to the curve \(f\) at \(t\). In the study of curves, it is usual (and convenient) to assume the existence of the tangent at every point of the curve:

Note that \(s'(t)=\left|f'(t)\right|\).

A regular parametrized curve is said to be parametrized by arc length if \(\left|f'(t)\right|=1\) for every \(t \in I\).

Assuming that a curve \(f\) determines the position of a certain particle, the fact that the curve is parametrized by arc length means that the particle is moving at constant speed \(1\).

Furthermore: the tangent vector \(T=\left(T_{1},T_{2}\right)\) to the curve at a certain \(t\) is given by \(f'(t)\) and the normal vector \(N=\left(N_{1},N_{2}\right)\) is given by \[\frac{f''(t)}{\left|f''(t)\right|}.\]

The definition of curvature that we present below is only valid for curves parametrized by arc length. This restriction is not really significative: given any smooth curve, it is possible to determine a differentiable curve parametrized by arc length which has the same trace as the given smooth curve.

Definition: Let \(f:\, I\rightarrow\mathbb{R}^{2}\) be a curve parametrized by arc length \(s \in I\). The curvature (with sign) of \(f\) is given by \[k(s)=§\left|f'(s)\right|\] where \(§\) is defined in the following way

Value of \(§\)	Condition	"Scheme"
\(§=1\)	\(T_{1}\times N_{2}-T_{2}\times N_{1} >0\)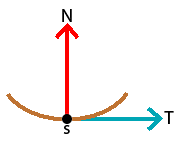
\(§=-1\)	\(T_{1}\times N_{2}-T_{2}\times N_{1} <0\)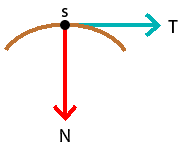