ATRACTOR

Designando por \(0, 1, 2\), respectivamente as hastes de baixo, da direita e da esquerda, vamos representar por \(i j\) o movimento do disco de cima da haste \(i\) para a haste \(j\), em que \(i, j\) são dois daqueles três números. Por exemplo, a solução do jogo, trivial no caso de existir um só disco, só terá um movimento e é representada por \(0 1\). No jogo com dois discos, a solução será \(02\)  \(01\)  \(21\), em que o disco mais pequeno vai para a haste vazia (\(2\)), depois move-se o disco grande para a haste \(1\) e finalmente o disco pequeno da haste \(2\) para a \(1\). Para maior clareza, escreveremos \(i j\) na cor do disco movido e usaremos tamanhos relativos de letras correspondendo aos tamanhos relativos dos discos movidos. Baseados nesta ideia, definimos uma função \(f\) que a um par \(i j\) num certo tamanho (e cor) faz corresponder um terno de pares \(ik\)  \(ij\)  \(kj\) tendo \(i k\) e \(k j\) uma cor contígua à usada para \(i j\) e sendo \(k\) o número de \(\{0,1,2\}\) diferente de \(i\) e de \(j\); e outra função \(g\) que, em cada lista de pares assim obtidos, substitui cada um dos pares \(m n\) da cor correspondente ao disco mais pequeno presente na lista pelo seu transformado por \(f\). Partindo de um só disco, temos como solução do jogo. Aplicando \(g\), temos e, aplicando \(g\) novamente, ou seja, substituindo cada par vermelho pela respectiva imagem por \(f\), temos 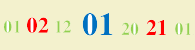. O segundo iterado de \(g\) aplicado a esta lista dá a lista representada na figura 7, que, para maior clareza, tem algumas linhas a envolver as diversas fases.

Fig. 7

As funções \(f\) e \(g\) podem ser utilizadas para construir a lista de movimentos da solução óptima para qualquer número de discos, por uma forma inteiramente automática, sem nenhum recurso explícito ao jogo, aos discos e às regras.

Página seguinte