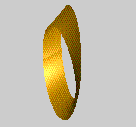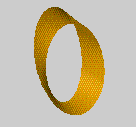Here is how to make a Möbius Band.

Many artists have been fascinated by the Möbius Band and by one sided figures. Here are two examples by Max Bill.

There are some nice Experiments YOU can do!

• Cut your Möbius Band down the middle. What results?
• Next cut your new strip down the middle again. What results?

• Make another Möbius Band. Cut it not down the middle but one third from the edge. What results?

• Form another strip of paper, and this time glue the ends together with a twist of 540 degrees. Again we have a surface with one edge and one side.
  It also is a Möbius Band, but the way it is put into our three dimensional space is different from the previous one.
  This makes an important distinction: between the object itself, and the way it is a part of a space.

• Cut this new object down the middle. What results?

There is another way of thinking of the structure of the Möbius Band, which corresponds to the way we made it from a strip. The Band has a middle circle, which goes round the Band only once. Notice that there are other circles, seemingly parallel to the middle one, but which go round the Band twice. Now draw lines on the Band at right angles to the middle circle. For each point of the middle circle we have a line, and as this line moves around the middle circle, it twists. This gives a mathematical model of the Möbius Band which we can realise in a picture. Here are four views of the Möbius Band. We can also produce a 3D rotating picture (90Kb) which we are extremely proud of !

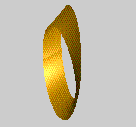
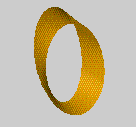
There is information explaining how we did these and the moving pictures, notes for doing the same with some of John Robinson's sculptures, and examples, such as a 3D rotating DEPENDENT BEINGS

We have also found another interesting picture of the Möbius Band, and it is in the Geometry Center Graphics Archive (outside link).

Here is another experiment, either in practice or a thought experiment. Make a  Möbius Band out of cloth, and make a disc of cloth whose edge is the same length as the edge of your Möbius Band. Now try and sew the two together along their edges. What happens?

What you are trying to make is called a Projective Plane.

THE MATHEMATICAL THEMES

• Borromean Rings - what they are and why they don't exist!
• Bernard Morin and the Brehm Model - how Bernard Morin showed John Robinson the Brehm Model of the Möbius Band and how to make one!
• The Projective Plane - how to create and understand the projective plane when it is not possible physically to construct it. We also describe the Brehm Model of the Projective Plane and the Dirac String Trick.
• Fibre Bundles - what they are, how to make them, and examples of them in John Robinson's work.
• Knots and Links - Introduction to the subject of Knot Theory, includes history of the subject, and a rotating mathematically constructed Immortality (the trefoil being one of the most basic knots).
• Torus Knots - two pages explaining the basics about torus knots with the help of colourful graphics. There are also 3D moving images of John Robinson's sculptures of the Gordian Knot and the Rhythm of Life.
• Fractals 3 pages, introducing Fractals, considering iteration, the Sierpinski Gasket and the applications of the subject.
• Exhibition "Mathematics and Knots"
• Ronnie Brown's Homepage
• John Robinson's Symbolic Sculpture
• Brochure giving a guided Tour around the Symbolic Sculptures at the University of Wales, Bangor.
• About the Centre for the Popularisation of Mathematics

Last modified 29 November, 1997.