KNOTS AND LINKS

The use of cordage by humans goes back into prehistory. The oldest known pierced object is over 300,000 years old, and was found in Austria in the Repolusthöhle.

This picture is taken from the book "History and Science of Knots"

It has been said that the Stone Age should be called the Age of String! The string itself quickly perished. The brain power which developed to see how to tie axes, spears, slings, to make fishing nets, to sew clothes, to bind vegetation for shelter, to improve chances of survival, and to decorate for enjoyment and display - is part of ourselves. This understanding of the form of a twisted line must be one of the oldest forms of applied geometry.

The use of knots, links and braids in art and imagery is a huge topic. There is the extraordinary interlacing of Celtic Art, of which the most famous is the Book of Kells. Myriads of examples occur across the world.

For mathematicians, the first study is the form of a knot, since other properties of interest to a practical knot tyer, as in the Ashley Book of Knots, are difficult to deal with mathematically, and in any case require first an understanding of form.

The start of the subject is the distinction between an unknotted and a knotted piece of string.

The knot cannot be untied without cutting the string, or letting go of one end. Since one gets tired of holding both ends, one ties them together to form a loop, so obtaining the trefoil knot, or its mirror image.

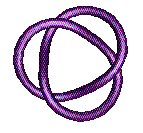
We have developed an Exhibition which shows how Mathematics gets into Knots, and which is also on the Web. Our pages on Torus Knots show some of the mathematics which John intuited in making his sculptures. In the following pictures, we see the sculpture CONSCIENCE contains the form of a trefoil knot.

Another trefoil knot used by John is in IMMORTALITY. This is more than a trefoil knot, it is actually a Möbius Band knotted into a trefoil. So it combines two mathematical themes discussed in these pages, knots and fibre bundles. Read again John's description of how he made IMMORTALITY to see this combination.

We have not been able to make an exact mathematical model of IMMORTALITY, but here is an approximation we have made.

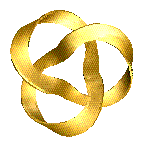To see this rotate, CLICK ON IT !

You will find other fascinating examples of M&oumlbius; Bands and twisted structures in Tom Longtin's pages (outside link). You will also find lots about knots in Knot Plot Site (outside link).

• Borromean Rings - what they are and why they don't exist!
• The Möbius Band - what one looks like, experiments to try, and a beautiful rotating golden one enabling you to really see what one looks like in 3D (this is optional as 90Kb).
• Bernard Morin and the Brehm Model - how Bernard Morin showed John Robinson the Brehm Model of the Möbius Band and how to make one!
• The Projective Plane (88Kb), (95Kb) - two pages explaining how to create and understand the projective plane although it is not possible physically to construct it. Also, the relation to the Brehm Model of the Möbius Band, and to the Dirac String Trick.
• Fibre Bundles - what they are, how to make them, and examples of them in John Robinson's Work.
• Torus Knots - two pages explaining the basics about torus knots with the help of full scale colour graphics. There are also 3D moving images of John Robinson's sculptures of the Gordian Knot and the Rhythm of Life.
• Fractals 3 pages, introducing Fractals, considering iteration, The Sierpinski Gasket and the applications of the subject.

• Exhibition "Mathematics and Knots"
• Ronnie Brown's Homepage
• John Robinson's Symbolic Sculpture
• Brochure giving a guided Tour around the Symbolic Sculptures at the University of Wales, Bangor.
• About the Centre for the Popularisation of Mathematics